Chứng minh rằng tứ giác ABCD là một hình bình hành khi và chỉ khi vecto BC = vecto AD
Câu hỏi:
Trả lời:
+) Nếu tứ giác ABCD là hình bình hành:
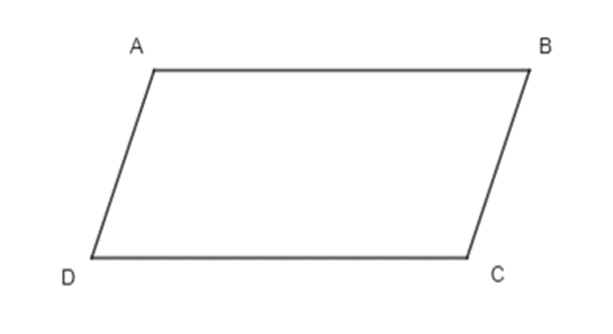
⇒ AD // BC (tính chất hình bình hành) và cùng phương và cùng hướng.
Mà AD = BC (tính chất hình bình hành)
+ Giả sử tứ giác ABCD có = suy ra cùng phương, cùng hướng và cùng độ dài.
Þ BC = AD (1) và AD, BC song song hoặc trùng nhau.
Nếu hai đường thẳng AD, BC trùng nhau thì bốn điểm A, B, C, D cùng nằm trên một đường thẳng, điều này không xảy ra vì ABCD là tứ giác. Vậy AD // BC. (2)
Từ (1) và (2) suy ra tứ giác ABCD là hình bình hành (dấu hiệu nhận biết).