Chuyển động của một vật thể trong khoảng thời gian 180 phút được thể hiện trong mặt phẳng tọa độ. Theo đó, tại thời điểm t (0 ≤ t ≤ 180) vật thể ở vị trí có tọa độ (2 + sint°; 4 + cost°). a)
Câu hỏi:
Chuyển động của một vật thể trong khoảng thời gian 180 phút được thể hiện trong mặt phẳng tọa độ. Theo đó, tại thời điểm t (0 ≤ t ≤ 180) vật thể ở vị trí có tọa độ (2 + sint°; 4 + cost°).
a) Tìm vị trí ban đầu và vị trí kết thúc của vật thể.
b) Tìm quỹ đạo chuyển động của vật thể.
Trả lời:
Hướng dẫn giải
a) Vị trí ban đầu của vật thể là tại thời điểm t = 0, nên tọa độ của điểm ở vị trí này là:
(2 + sin0°; 4 + cos0°) = (2; 5).
Vị trí kết thúc của vật thể là tại thời điểm t = 180, nên tọa độ của điểm ở vị trí này là:
(2 + sin 180°; 4 + cos 180°) = (2; 3).
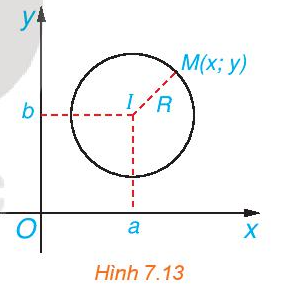
b) Gọi điểm M(x; y) thuộc vào quỹ đạo chuyển động của vật thể.
Ta có: x = 2 + sin t° và y = 4 + cost°.
Suy ra: x – 2 = sin t° và y – 4 = cost°.
Mà sin2 t° + cos2 t° = 1 (0 ≤ t ≤ 180)
Do đó ta có: (x – 2)2 + (y – 4)2 = 1.
Vậy vật thể chuyển động trên đường tròn có tâm I(2; 4) và bán kính R = 1.
Vị trí ban đầu của vật thể là A(2; 5), vị trí kết thúc của vật thể là B(2; 3).
Ta có nên I là trung điểm của AB
Và .
Do đó vật thể chuyển động trên đường tròn có tâm I(2; 4), bán kính R = 1 và nhận AB làm đường kính.
Khi t thay đổi trên đoạn [0; 180] thì sin t° thay đổi trên đoạn [0; 1] và cos t° thay đổi trên đoạn [– 1; 1]. Do đó 2 + sin t° ∈ [2; 3] và 4 + cos t° ∈ [3; 5].
Vậy quỹ đạo của vật thể (hay là tập hợp điểm M) là nửa đường tròn đường kính AB vẽ trên nửa mặt phẳng chứa điểm C(3; 0), bờ AB.