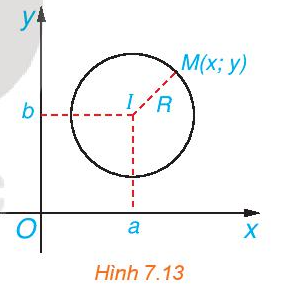
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C), tâm I(a; b), bán kính R (H.7.13). Khi đó, một điểm M(x; y) thuộc đường tròn (C) khi và chỉ khi tọa độ của nó thỏa mãn điều kiện đại số nào?

Hướng dẫn giải

Điểm M thuộc đường tròn (C) khi khoảng cách từ tâm I của (C) đến M bằng bán kính R của (C).

Ta có: \(\overrightarrow {IM} = \left( {x - a;y - b} \right)\) nên \(IM = \sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2}} \).

Khi đó IM = R \( \Leftrightarrow \sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2}} = R\)\( \Leftrightarrow {\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\) (do R > 0, (x – a)² ≥ 0, (y – b)² ≥ 0).

Vậy điểm M(x; y) thuộc đường tròn (C), tâm I(a; b), bán kính R khi và chỉ khi

(x – a)² + (y – b)² = R².