Giá trị lớn nhất của biểu thức F(x; y) = 2x + y trên miền xác định bởi hệ:

Giá trị lớn nhất của biểu thức F(x; y) = 2x + y trên miền xác định bởi hệ: $\left\{\begin{array}{c}y-2x\le 2\\ 2y-x\ge 4\\ x+y\le 5\end{array}\right.$  là:

A. max F(x; y) = 1 khi x = 2, y = - 3;

Hướng dẫn giải

Đáp án Đúng là: D

Ta tìm miền nghiệm xác định bởi hệ $\left\{\begin{array}{c}y-2x\le 2\\ 2y-x\ge 4\\ x+y\le 5\end{array}\right.$

Vẽ đường thẳng d₁: y – 2x = 2, đường thẳng d₁ qua hai điểm (0; 2) và (– 1; 0).

Ta xét điểm O(0; 0) thay vào phương trình đường thẳng ta có  0 – 2.0 = 0 < 2.

Do đó điểm O(0; 0) thuộc miền nghiệm của bất phương trình. Vậy miền nghiệm D₁ là nửa mặt phẳng được chia bởi đường thẳng d₁ chứa gốc tọa độ O kể cả bờ.

Vẽ đường thẳng d₂: 2y – x = 4, đường thẳng d₂ qua hai điểm (0; 2) và (– 4; 0).

Ta xét điểm O(0; 0) thay vào phương trình đường thẳng ta có 2.0 – 0 = 0 < 4 không thoả mãn bất phương trình 2y – x ≥ 4.

Do đó điểm O(0; 0) không thuộc nềm nghiệm của bất phương trình. Vậy miền nghiệm D₂ là nửa mặt phẳng được chia bởi đường thẳng d₂ không chứa gốc tọa độ O kể cả bờ.

Vẽ đường thẳng d₃: x + y = 5, đường thẳng d₁ qua hai điểm (0; 5) và (5; 0).

Xét điểm O(0; 0) thay vào phương trình đường thẳng ta có 0 + 0 = 0 < 5, thoả mãn bất phương trình x + y ≤ 5.

Do đó điểm O(0; 0) thuộc miền nghiệm của bất phương trình. Vậy miền nghiệm D₃ là nửa mặt phẳng được chia bởi đường thẳng d₃ chứa gốc tọa độ O kể cả bờ.

Miền nghiệm là phần không gạch chéo như hình vẽ.

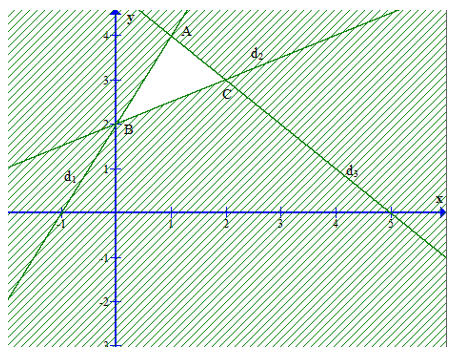
Miền nghiệm là tam giác ABC với A(1; 4), B(0; 2), C(2; 3).

Ta tính giá trị của F(x; y) = 2x + y tại các giao điểm:

Tính F(x; y) = 2x + y suy ra F(1; 4) = 2.1 + 4 = 6.

Tính F(x; y) = 2x + y suy ra F(0; 2) = 2.0 + 2 = 2.

Tính F(x; y) = 2x + y suy ra F(2; 3) = 2.2 + 3 = 7.

Vậy max F(x; y) = 7 khi x = 2, y = 3.