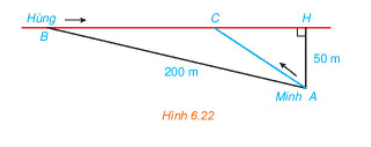
Hằng ngày bạn Hùng đều đón bạn Minh đi học tại một vị trí trên lề đường thẳng đến trường. Minh đứng tại vị trí A cách lề đường một khoảng 50 m để chờ Hùng. Khi nhìn thấy Hùng đạp xe đến địa đ

Đổi: 200 m = 0,2 km, 50 m = 0,05 km.

Đặt CH = x (km) (x > 0).

Xét tam giác CHA vuông tại H, theo định lí Pythagore ta có:

CA² = HA² + HC² = (0,05)² + x² = 0,0025 + x²

Suy ra CA = $\sqrt{\mathrm{0,0025}+x^2}$ hay quãng đường di chuyển của Minh từ vị trí A đến điểm gặp nhau C dài $\sqrt{\mathrm{0,0025}+x^2}$ km.

Vận tốc đi bộ của Minh là 5 km/h nên thời gian di chuyển của Minh từ vị trí A đến điểm gặp nhau C là: $\frac{\sqrt{\mathrm{0,0025}+x^2}}{5}$ (giờ).

Xét tam giác HAB vuông tại H, theo định lí Pythagore ta có:

AB² = HB² + HA² ⇔ HB² = AB² – HA² = (0,2)² – (0,05)² = 0,0375

Suy ra HB = $\frac{\sqrt{15}}{20}$.

Ta có: BC + CH = HB ⇔ BC = HB – CH = $\frac{\sqrt{15}}{20}-x$.

Do đó quãng đường di chuyển của Hùng từ B đến điểm gặp nhau C dài $\frac{\sqrt{15}}{20}-x$ km.

Vận tốc đạp xe của Hùng là 15 km/h nên thời gian di chuyển của Hùng từ B đến điểm gặp nhau là: $\frac{\frac{\sqrt{15}}{20}-x}{15}=\frac{\sqrt{15}-20x}{300}$ (giờ).

Để hai bạn gặp nhau mà không bạn nào phải chờ người kia thì thời gian di chuyển từ vị trí A đến C của Minh phải bằng thời gian di chuyển từ vị trí B đến C của Hùng.

Khi đó ta có phương trình: $\frac{\sqrt{\mathrm{0,0025}+x^2}}{5}=\frac{\sqrt{15}-20x}{300}$    (1).

Giải phương trình (1) ta có:

(1) $\iff 60\sqrt{\mathrm{0,0025}+x^2}=\sqrt{15}-20x$

Bình phương hai vế của phương trình trên ta được:

3600.(0,0025 + x²) = 15 – 40$\sqrt{15}$x + 400x²

⇔ 3200x² + 40$\sqrt{15}$x – 6 = 0

⇔ x = $\frac{-\sqrt{15}-3\sqrt{7}}{160}$ hoặc x = $\frac{-\sqrt{15}+3\sqrt{7}}{160}$

Thay lần lượt các giá trị này vào phương trình (1) ta thấy cả hai giá trị đều thỏa mãn.

Lại có điều kiện của x là x > 0 nên ta chọn x = $\frac{-\sqrt{15}+3\sqrt{7}}{160}$≈ 0,0254.

Suy ra BC = BH – CH ≈ $\frac{\sqrt{15}}{20}-\mathrm{0,0254}\approx \mathrm{0,1682}$ km = 168,2 m.

Vậy vị trí C thỏa mãn yêu cầu đề bài là điểm cách B khoảng 168,2 m.