Hình bình hành ABCD có AB = a; BC = a căn bậc hai 2 và góc BAD = 45 độ

Câu hỏi:

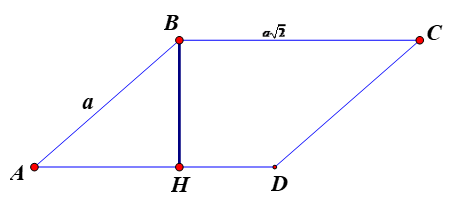
Hình bình hành ABCD có AB = a; \(BC = a\sqrt 2 \) và \(\widehat {BAD} = 45^\circ \). Khi đó hình bình hành có diện tích bằng

A. 2a²;

B. \({a^2}\sqrt 2 \);

C. a²;

D. \({a^2}\sqrt 3 \).

Trả lời:

Đáp án đúng là: C

Gọi BH là đường cao của hình bình hành ABCD.

Tam giác BAH vuông tại H, góc \(\widehat {BAH} = \widehat {BAD} = 45^\circ \),

Ta có BH = AB.sin45° = \(\frac{{a\sqrt 2 }}{2}\).

Diện tích hình bình hành ABCD là: \(S = BH.AD = \frac{{a\sqrt 2 }}{2}.a\sqrt 2 = {a^2}\)(đvdt).

Câu 1:

Tính diện tích tam giác có ba cạnh lần lượt là 5; 12; 13.

Câu 2:

Tam giác ABC có \(AC = 3\sqrt 3 \), AB = 3, BC = 6. Tính số đo góc B

Câu 3:

Tam giác ABC có các góc \(\widehat A = 75^\circ ,\widehat B = 45^\circ \). Tính tỉ số \(\frac{{AB}}{{AC}}\).

Câu 4:

Tam giác ABC có các góc \(\widehat B = 30^\circ ,\widehat C = 45^\circ \), AB = 3. Tính cạnh AC.

Câu 5:

Tính góc C của tam giác ABC biết a ≠ b và a(a² – c²) = b(b² – c²).

Câu 6:

Tam giác ABC có các cạnh a; b; c thỏa mãn điều kiện:

(a + b + c)(a + b – c) = 3ab. Khi đó số đo của góc C là.

Câu 7:

Tam giác ABC có AB = 7; AC = 5 và \(\cos \left( {B + C} \right) = - \frac{1}{5}\). Tính BC

Câu 8:

Hình bình hành có hai cạnh là 3 và 5, một đường chéo bằng 5. Tìm độ dài đường chéo còn lại.

<<<<<<< HEAD ======= >>>>>>> 7de0ce75c76253c52280308e94cf2d713ccea5e2

Giải Toán 10 Kết nối tri thức