Tích vô hướng của hai vectơ (Lý thuyết Toán lớp 10) | Kết nối tri thức

❮ Bài trước Bài sau ❯

Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán 10 Bài 11: Tích vô hướng của hai vectơ sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 10.

Trắc nghiệm Toán 10 Bài 11: Tích vô hướng của hai vectơ (có đáp án)

Tích vô hướng của hai vectơ (Lý thuyết Toán lớp 10) | Kết nối tri thức

Lý thuyết Tích vô hướng của hai vectơ

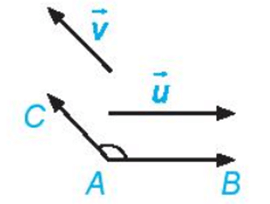
1. Góc giữa hai vectơ

Cho hai vectơ $\vec{u}$ và $\vec{v}$ khác $\vec{0}$ . Từ một điểm A tùy ý, vẽ các vectơ $\vec{A B} = \vec{u}$ và $\vec{A C} = \vec{v}$ . Khi đó, số đo của góc BAC được gọi là số đo góc giữa hai vectơ $\vec{u}$ và $\vec{v}$ hay đơn giản là góc giữa hai vectơ $\vec{u}$ , $\vec{v}$ , kí hiệu là ( $\vec{u}$ , $\vec{v}$ ).

Chú ý :

+ Quy ước rằng góc giữa hai vectơ $\vec{u}$ và $\vec{0}$ có thể nhận một giá trị tùy ý từ 0° đến 180°.

+ Nếu ( $\vec{u}$ , $\vec{v}$ ) = 90° thì ta nói rằng $\vec{u}$ và $\vec{v}$ vuông góc với nhau. Kí hiệu $\vec{u}$ ⊥ $\vec{v}$ hoặc $\vec{v}$ ⊥ $\vec{u}$ . Đặc biệt được coi là vuông góc với mọi vectơ.

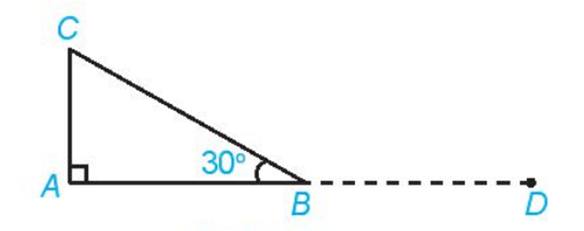
Ví dụ : Cho tam giác ABC vuông tại A và $\hat{B} = 30 °$ . Tính $(\vec{A B}, \vec{A C})$ , $(\vec{C A}, \vec{C B})$ , $(\vec{A B}, \vec{B C})$ .

Hướng dẫn giải

Ta có $(\vec{A B}, \vec{A C})$ = $\hat{B A C} = 90 °$ .

Tam giác ABC vuông tại A nên ta có .

$\hat{A C B} + \hat{A B C} = 90 ° \Rightarrow \hat{A C B} = 90 ° - \hat{A B C} = 90 ° - 30 ° = 60 °$

Suy ra: $(\vec{C A}, \vec{C B}) = \hat{A C B} = 60 °$ .

Vẽ $\vec{B D}$ sao cho $\vec{B D}$ = $\vec{A B}$ . Khi đó $(\vec{A B}, \vec{B C})$ = $(\vec{B D}, \vec{B C})$ = $\hat{C B D}$ .

Mặt khác $\hat{A B C} + \hat{C B D} = 180 °$ (hai góc kề bù)

Suy ra $\hat{C B D} = 180 ° - \hat{A B C} = 180 ° - 30 ° = 150 °$ .

Do đó, $(\vec{A B}, \vec{B C})$ = $\hat{C B D}$ = 150°.

Vậy $(\vec{A B}, \vec{A C})$ = 90°, $(\vec{C A}, \vec{C B})$ = 60°, $(\vec{A B}, \vec{B C})$ = 150°.

2. Tích vô hướng của hai vectơ

Tích vô hướng của hai vectơ khác vectơ-không $\vec{u}$ và $\vec{v}$ là một số, kí hiệu là $\vec{u}$ . $\vec{v}$ , được xác định bởi công thức sau:

$\vec{u}$ . $\vec{v}$ = | $\vec{u}$ |.| $\vec{v}$ |.cos( $\vec{u}$ , $\vec{v}$ )

Chú ý:

+) $\vec{u}$ ⊥ $\vec{v}$ ⇔ $\vec{u}$ . $\vec{v}$ = 0.

+) $\vec{u}$ . $\vec{u}$ còn được viết là ${\vec{u}}^{2}$ và được gọi là bình phương vô hướng của vectơ $\vec{u}$ .

Ta có ${\vec{u}}^{2} = | \vec{u} | . | \vec{u} | . \cos 0 ° = {(\vec{u})}^{2}$ .

(Bình phương vô hướng của một vectơ bằng bình phương độ dài của vectơ đó.)

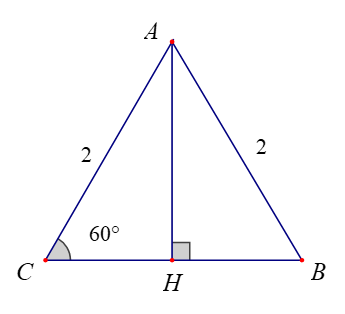
Ví dụ: Cho tam giác đều ABC có cạnh bằng 2 và có đường cao AH. Tính các tích vô hướng:

a) $\vec{A B} . \vec{A C}$ ;

b) $\vec{A H} . \vec{B C}$ .

Hướng dẫn giải

Tích vô hướng của hai vectơ (Lý thuyết Toán lớp 10) | Kết nối tri thức

a) Vì tam giác ABC đều nên $(\vec{A B}, \vec{A C}) = \hat{B A C} = 60 °$ .

Suy ra: $\vec{A B} . \vec{A C} = | \vec{A B} | . | \vec{A C} | \cos (\vec{A B}, \vec{A C}) = 2.2. \cos 60 ° = 2.2. \frac{1}{2} = 2$ .

Vậy $\vec{A B} . \vec{A C}$ = 2.

b) Vì AH là đường cao của tam giác ABC nên AH ⊥ BC.

Do đó $(\vec{A H}, \vec{B C}) = 90 °$ .

Ta có: $\vec{A H} . \vec{B C} = | \vec{A H} | . | \vec{B C} | \cos (\vec{A H}, \vec{B C}) = | \vec{A H} | . | \vec{B C} | \cos 90 ° = | \vec{A H} | . | \vec{B C} | .0 = 0$ .

Vậy $\vec{A H} . \vec{B C}$ = 0.

3. Biểu thức tọa độ và tính chất của tích vô hướng

• Tích vô hướng của hai vectơ $\vec{u} = (x; y)$ và $\vec{v} = (x'; y')$ được tính theo công thức :

$\vec{u}$ . $\vec{v}$ = x.x' + y.y'.

Nhận xét:

+ Hai vectơ $\vec{u}$ và $\vec{v}$ vuông góc với nhau khi và chỉ khi x.x' + y.y' = 0.

+ Bình phương vô hướng của $\vec{u} = (x; y)$ là ${\vec{u}}^{2}$ = x² + y².

+ Nếu $\vec{u}$ ≠ $\vec{0}$ và $\vec{v}$ ≠ $\vec{0}$ thì cos( $\vec{u}$ , $\vec{v}$ ) = $\frac{\vec{u} . \vec{v}}{| \vec{u} | . | \vec{v} |} = \frac{x x' + y y'}{\sqrt{x^{2} + y^{2}} . \sqrt{x'^{2} + y'^{2}}}$ .

Ví dụ: Trong mặt phẳng tọa độ cho hai vectơ $\vec{u} = (0; - 5)$ và $\vec{v} = (\sqrt{3}; 1)$ .

a) Tính tích vô hướng của hai vectơ trên.

b) Tìm góc giữa của hai vectơ trên.

Hướng dẫn giải

a) Ta có: $\vec{u}$ . $\vec{v}$ = 0. $\sqrt{3}$ + (–5).1= –5;

Vậy $\vec{u}$ . $\vec{v}$ = –5.

b) Ta có $| \vec{u |} = \sqrt{0^{2} + {(- 5)}^{2}} = 5$ ; $| \vec{v} | = \sqrt{{(\sqrt{3})}^{2} + 1^{2}} = 2$

Suy ra : cos( $\vec{u}$ , $\vec{v}$ ) = $\frac{\vec{u} . \vec{v}}{| \vec{u} | . | \vec{v} |} = \frac{- 5}{5.2} = \frac{- 5}{10} = \frac{- 1}{2}$ .

Suy ra ( $\vec{u}$ , $\vec{v}$ ) = 120°.

Vậy ( $\vec{u}$ , $\vec{v}$ ) = 120°.

• Tính chất của tích vô hướng :

Với ba vectơ $\vec{u}$ , $\vec{v}$ , $\vec{w}$ bất kì và mọi số thực k, ta có :

+) $\vec{u}$ . $\vec{v}$ = $\vec{v}$ . $\vec{u}$ (tính chất giao hoán);

+) $\vec{u}$ . ( $\vec{v}$ + $\vec{w}$ ) = $\vec{u}$ . $\vec{v}$ + $\vec{u}$ . $\vec{w}$ (tính chất phân phối đối với phép cộng) ;

+) (k $\vec{u}$ ). $\vec{v}$ = k ( $\vec{u}$ . $\vec{v}$ ) = $\vec{u}$ .( k $\vec{v}$ ).

Chú ý: Từ tính trên, ta có thể chứng minh được :

$\vec{u}$ . ( $\vec{v}$ – $\vec{w}$ )= $\vec{u}$ . $\vec{v}$ – $\vec{u}$ . $\vec{w}$ (tính chất phân phối đối với phép trừ) ;

( $\vec{u}$ + $\vec{v}$ )² = ${\vec{u}}^{2}$ + 2 $\vec{u}$ . $\vec{v}$ + ${\vec{v}}^{2}$ ; ( $\vec{u}$ – $\vec{v}$ )² = ${\vec{u}}^{2}$ –2 $\vec{u}$ . $\vec{v}$ + ${\vec{v}}^{2}$ ;

( $\vec{u}$ + $\vec{v}$ ).( $\vec{u}$ – $\vec{v}$ ) = ${\vec{u}}^{2}$ – ${\vec{v}}^{2}$ .

Ví dụ: Cho tam giác ABC. Chứng minh rằng với điểm M tùy ý ta có:

$\vec{M A} . \vec{B C} + \vec{M B} . \vec{C A} + \vec{M C} . \vec{A B} = 0$ .

Hướng dẫn giải

Ta có $\vec{M A} . \vec{B C} = \vec{M A} . (\vec{M C} - \vec{M B}) = \vec{M A} . \vec{M C} - \vec{M A} . \vec{M B};$ (1)

$\vec{M B} . \vec{C A} = \vec{M B} . (\vec{M A} - \vec{M C}) = \vec{M B} . \vec{M A} - \vec{M B} . \vec{M C};$ (2)

$\vec{M C} . \vec{A B} = \vec{M C} . (\vec{M B} - \vec{M A}) = \vec{M C} . \vec{M B} - \vec{M C} . \vec{M A}$ . (3)

Cộng các kết quả từ (1), (2), (3), ta được: $\vec{M A} . \vec{B C} + \vec{M B} . \vec{C A} + \vec{M C} . \vec{A B} = 0$

Vậy $\vec{M A} . \vec{B C} + \vec{M B} . \vec{C A} + \vec{M C} . \vec{A B} = 0$ .

Bài tập Tích vô hướng của hai vectơ

Bài 1: Cho hai vectơ $\vec{a} = (1; - 2); \vec{b} = (- 1; - 3)$ .

a) Tính tích vô hướng của $\vec{a}$ và $\vec{b}$ .

b) Tính góc giữa hai vectơ $\vec{a}$ và $\vec{b}$ .

Hướng dẫn giải

a) Ta có $\vec{a}$ . $\vec{b}$ = 1.(–1) + (–2).(–3) = 5.

Vậy $\vec{a}$ . $\vec{b}$ = 5.

b) Ta có $| \vec{a} | = \sqrt{1^{2} + {(- 2)}^{2}} = \sqrt{5}$ ; $| \vec{b} | = \sqrt{{(- 1)}^{2} + {(- 3)}^{2}} = \sqrt{10}$ .

Khi đó cos( $\vec{a}$ , $\vec{b}$ ) = $\frac{\vec{a} . \vec{b}}{| \vec{a} | . | \vec{b} |} = \frac{5}{\sqrt{5} . \sqrt{10}} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}$ .

Suy ra ( $\vec{a}$ , $\vec{b}$ ) = 45°.

Vậy góc giữa hai vectơ và là 45°.

Bài 2: Trong mặt phẳng tọa độ Oxy cho hai điểm A(2; 4) và B(1; 1). Tìm tọa độ của điểm C sao cho tam giác ABC là tam giác vuông cân tại B.

Hướng dẫn giải

Giả sử điểm C cần tìm có tọa độ (x; y). Để tam giác ABC vuông cân tại B ta phải có:

$(\begin{matrix} \vec{B A} . \vec{B C} = 0 \\ | \vec{B A} | = | \vec{B C} | \end{matrix})$

Ta có $\vec{B A} = (1; 3)$ và $\vec{B C} = (x - 1; y - 1)$ .

Khi đó $\vec{B A} . \vec{B C} = 1. (x - 1) + 3 (y - 1) = x + 3 y - 4$ .

Và $| \vec{B A} | = \sqrt{1^{2} + 3^{2}} = \sqrt{10}$ ; $| \vec{B C} | = \sqrt{{(x - 1)}^{2} + {(y - 1)}^{2}}$

Ta có: $(\begin{matrix} \vec{B A} . \vec{B C} = 0 \\ | \vec{B A} | = | \vec{B C} | \end{matrix})$

⇔ $(\begin{matrix} x + 3 y - 4 = 0 \\ \sqrt{10} = \sqrt{{(x - 1)}^{2} + {(y - 1)}^{2}} \end{matrix})$

⇔ $(\begin{matrix} x + 3 y - 4 = 0 \\ 10 = {(x - 1)}^{2} + {(y - 1)}^{2} \end{matrix})$

⇔ $(\begin{matrix} x = 4 - 3 y \\ {(3 - 3 y)}^{2} + {(y - 1)}^{2} = 10 \end{matrix}) \Leftrightarrow (\begin{matrix} x = 4 - 3 y \\ 10 y^{2} - 20 y = 0 \end{matrix})$

⇔ $(\begin{matrix} x = 4 - 3 y \\ (\begin{matrix} y = 0 \\ y = 2 \end{matrix}) \end{matrix})$ ⇔ $(\begin{matrix} (\begin{matrix} x = 4 \\ y = 0 \end{matrix}) \\ (\begin{matrix} x = - 2 \\ y = 2 \end{matrix}) \end{matrix})$