Tích của một vectơ với một số (Lý thuyết Toán lớp 10) | Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán 10 Bài 9: Tích của một vectơ với một số sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 10.

Tích của một vectơ với một số (Lý thuyết Toán lớp 10) | Kết nối tri thức

Lý thuyết Tích của một vectơ với một số

1. Tích của một vectơ với một số

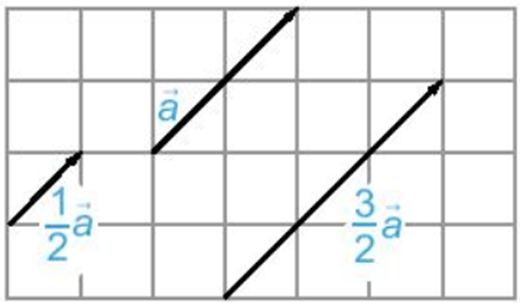
• Tích của một vectơ $\overrightarrow{a}\ne \overrightarrow{0}$ với một số thực k > 0 là một vectơ, kí hiệu là k $\overrightarrow{a}$, cùng hướng với vectơ $\overrightarrow{a}$ và có độ dài bằng k $\overrightarrow{a}$.

Ví dụ: Cho hình vẽ sau:

– Vectơ $\frac{1}{2}\overrightarrow{a}$ cùng hướng với vectơ $\overrightarrow{a}$ và $\left(\frac{1}{2}\overrightarrow{a}\right)$ = $\frac{1}{2}\left|\overrightarrow{a}\right|$

– Vectơ $\frac{3}{2}\overrightarrow{a}$ cùng hướng với vectơ $\overrightarrow{a}$ và $\left(\frac{3}{2}\overrightarrow{a}\right)$= $\frac{3}{2}\left|\overrightarrow{a}\right|$.

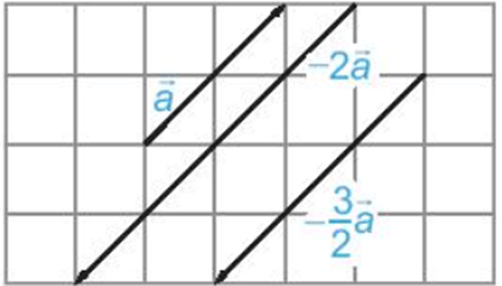
• Tích của một vectơ $\overrightarrow{a}\ne \overrightarrow{0}$ với một số thực k < 0 là một vectơ, kí hiệu là k $\overrightarrow{a}$, ngược hướng với vectơ $\overrightarrow{a}$ và có độ dài bằng (–k) |$\overrightarrow{a}$|.

Ví dụ: Cho hình sau:

– Vectơ –2$\overrightarrow{a}$ ngược hướng với vectơ $\overrightarrow{a}$ và $\left(-2\overrightarrow{a}\right)$= $2\left|\overrightarrow{a}\right|$

– Vectơ $-\frac{3}{2}\overrightarrow{a}$ ngược hướng với vectơ $\overrightarrow{a}$ và $\left(-\frac{3}{2}\overrightarrow{a}\right)$= $\frac{3}{2}\left|\overrightarrow{a}\right|$.

Chú ý: Ta quy ước k $\overrightarrow{a}$ = $\overrightarrow{0}$ nếu $\overrightarrow{a}$ = $\overrightarrow{0}$ hoặc k = 0.

Nhận xét: Vectơ k $\overrightarrow{a}$ có độ dài bằng |k||$\overrightarrow{a}$| và cùng hướng với $\overrightarrow{a}$ nếu k ≥ 0, ngược hướng với $\overrightarrow{a}$ nếu $\overrightarrow{a}$ ≠ $\overrightarrow{0}$ và k < 0.

Chú ý: Phép lấy tích của vectơ với một số gọi là phép nhân vectơ với một số (hay phép nhân một số với vectơ).

2. Các tính chất của phép nhân vectơ với một số

Với hai vectơ $\overrightarrow{a}$, $\overrightarrow{b}$ và hai số thực k, t, ta luôn có :

+) k(t$\overrightarrow{a}$) = (kt) $\overrightarrow{a}$;

+) k ($\overrightarrow{a}$ + $\overrightarrow{b}$) = k$\overrightarrow{a}$ + k$\overrightarrow{b}$; k ($\overrightarrow{a}$ – $\overrightarrow{b}$) = k$\overrightarrow{a}$ – k$\overrightarrow{b}$;

+) (k + t) $\overrightarrow{a}$ = k$\overrightarrow{a}$ + t$\overrightarrow{a}$;

+) 1$\overrightarrow{a}$ = $\overrightarrow{a}$; (–1) $\overrightarrow{a}$ = –$\overrightarrow{a}$.

Nhận xét:

Điểm I là trung điểm của đoạn thẳng AB khi và chỉ khi $\overrightarrow{IA}+\overrightarrow{IB}=\overrightarrow{0}$.

Điểm G là trọng tâm của tam giác ABC khi và chỉ khi $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$.

Ví dụ:

a) Cho đoạn thẳng CD có trung điểm I. Chứng minh với điểm O tùy ý, ta có $\overrightarrow{OC}+\overrightarrow{OD}=2\overrightarrow{OI}$.

b) Cho tam giác ABC có G là trọng tâm. Chứng minh rằng với điểm O tùy ý, ta có $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=3\overrightarrow{OG}$.

Hướng dẫn giải

a) Vì I là trung điểm của CD nên ta có $\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}$.

Do đó $\overrightarrow{OC}+\overrightarrow{OD}=(\overrightarrow{OI}+\overrightarrow{IC})+(\overrightarrow{OI}+\overrightarrow{ID})$ = 2$\overrightarrow{OI}$ + ($\overrightarrow{IC}+\overrightarrow{ID}$)= 2$\overrightarrow{OI}$ + $\overrightarrow{0}$ = 2$\overrightarrow{OI}$.

Vậy, $\overrightarrow{OC}+\overrightarrow{OD}=2\overrightarrow{OI}$.

b) Vì G là trọng tâm tam giác ABC nên: $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$.

Ta có $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=(\overrightarrow{OG}+\overrightarrow{GA})+(\overrightarrow{OG}+\overrightarrow{GB})+(\overrightarrow{OG}+\overrightarrow{GC})$

= $3\overrightarrow{OG}+(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC})=3\overrightarrow{OG}+\overrightarrow{0}=3\overrightarrow{OG}$

Vậy $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=3\overrightarrow{OG}$.

Chú ý : Cho hai vectơ không cùng phương $\overrightarrow{a}$ và $\overrightarrow{b}$. Khi đó, mọi vectơ $\overrightarrow{u}$ đều biểu thị (phân tích) được một cách duy nhất theo hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$, nghĩa là có duy nhất cặp số (x; y) sao cho $\overrightarrow{u}$ = x$\overrightarrow{a}$ + y$\overrightarrow{b}$.

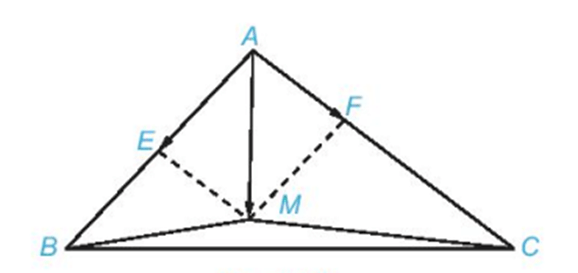
Ví dụ : Cho tam giác ABC. Hãy xác định điểm M để $\overrightarrow{MA}+3\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{0}$.

Hướng dẫn giải

Để xác định vị trí của M, trước hết ta biểu thị $\overrightarrow{AM}$ (với gốc A đã biết) theo hai vectơ đã biết $\overrightarrow{AB},\overrightarrow{AC}$.

$\overrightarrow{MA}+3\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{0}$

⇔ $\overrightarrow{MA}+3(\overrightarrow{MA}+\overrightarrow{AB})+2(\overrightarrow{MA}+\overrightarrow{AC})=\overrightarrow{0}$

⇔ $6\overrightarrow{MA}+3\overrightarrow{AB}+2\overrightarrow{AC}=\overrightarrow{0}$

⇔ $\overrightarrow{AM}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$

Lấy điểm E là trung điểm của AB và điểm F thuộc cạnh AC sao cho $\text{AF}=\frac{1}{3}AC$.

Khi đó $\overrightarrow{AE}=\frac{1}{2}\overrightarrow{AB}$ và $\overrightarrow{AF}=\frac{1}{3}\overrightarrow{AC}$. Vì vậy $\overrightarrow{AM}=\overrightarrow{AE}+\overrightarrow{AF}$.

Suy ra M là đỉnh thứ tư của hình bình hành EAFM.

Bài tập Tích của một vectơ với một số

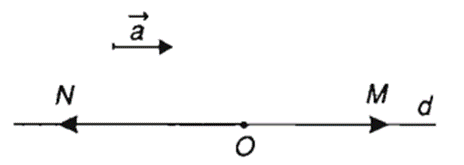
Bài 1: Cho $\overrightarrow{a}$ và điểm O không thuộc giá của $\overrightarrow{a}$. Xác định hai điểm M và N sao cho $\overrightarrow{OM}=3\overrightarrow{a},\overrightarrow{ON}=-4\overrightarrow{a}$.

Hướng dẫn giải

Vẽ đường thẳng d đi qua O và song song với giá của $\overrightarrow{a}$.

Trên d lấy điểm M sao cho OM= 3|$\overrightarrow{a}$|, $\overrightarrow{OM}$ và $\overrightarrow{a}$ cùng hướng khi đó $\overrightarrow{OM}=3\overrightarrow{a}$.

Trên d lấy điểm N sao cho ON = 4|$\overrightarrow{a}$|, $\overrightarrow{ON}$ và $\overrightarrow{a}$ ngược hướng, khi đó $\overrightarrow{ON}=-4\overrightarrow{a}$.

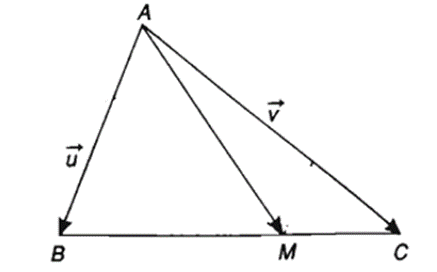
Bài 2: Cho tam giác ABC. Điểm M trên cạnh BC sao cho MB = 2MC. Hãy phân tích vectơ $\overrightarrow{AM}$ theo hai vectơ $\overrightarrow{u}=\overrightarrow{AB},\overrightarrow{v}=\overrightarrow{AC}$.

Hướng dẫn giải

Ta có: $\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{AB}+\frac{2}{3}\overrightarrow{BC}$

= $\overrightarrow{AB}+\frac{2}{3}(\overrightarrow{AC}-\overrightarrow{AB})=\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}$

Vậy $\overrightarrow{AM}=\frac{1}{3}\overrightarrow{u}+\frac{2}{3}\overrightarrow{v}$.

Bài 3: Cho tam giác ABC. Hai điểm M, N được xác định bởi các hệ thức: $\overrightarrow{BC}+\overrightarrow{MA}=\overrightarrow{0},\overrightarrow{AB}-\overrightarrow{NA}-3\overrightarrow{AC}=\overrightarrow{0}$. Chứng minh MN // AC.

Hướng dẫn giải

Vì $\overrightarrow{BC}+\overrightarrow{MA}=\overrightarrow{0},\overrightarrow{AB}-\overrightarrow{NA}-3\overrightarrow{AC}=\overrightarrow{0}$

Do đó ta có: $\overrightarrow{BC}+\overrightarrow{MA}+\overrightarrow{AB}-\overrightarrow{NA}-3\overrightarrow{AC}=\overrightarrow{0}$

Hay $(\overrightarrow{AB}+\overrightarrow{BC})+(\overrightarrow{MA}+\overrightarrow{AN})-3\overrightarrow{AC}=\overrightarrow{0}$

⇔ $\overrightarrow{AC}+\overrightarrow{MN}-3\overrightarrow{AC}=\overrightarrow{0}$

⇔ $\overrightarrow{MN}=2\overrightarrow{AC}$

Vậy $\overrightarrow{MN}$ và $\overrightarrow{AC}$ cùng phương.

Từ giả thiết $\overrightarrow{BC}+\overrightarrow{MA}=\overrightarrow{0}$ suy ra $\overrightarrow{BC}=\overrightarrow{AM}$, mà A, B, C không thẳng hàng nên bốn điểm A, B, C, M là 4 đỉnh của một hình bình hành.

Suy ra M không thuộc đường thẳng AC, mà $\overrightarrow{MN}$ và $\overrightarrow{AC}$ cùng phương.

Vậy MN // AC.

Học tốt Tích của một vectơ với một số

Các bài học để học tốt Tích của một vectơ với một số Toán lớp 10 hay khác:

• Giải sgk Toán 10 Bài 9: Tích của một vectơ với một số