Tại sao trong định nghĩa hypebol cần điều kiện a < c?

A. Các câu hỏi trong bài

Đính hai đầu của một sợi dây không đàn hồi vào hai vị trí cố định F₁, F₂ trên một mặt bàn (độ dài sợi dây lớn hơn khoảng cách giữa hai điểm F₁, F₂ ). Kéo căng sợi dây tại một điểm M bởi một đầu bút dạ (hoặc phấn). Di chuyển đầu bút dạ để nó vẽ trên mặt bàn một đường khép kín (H.7.18).

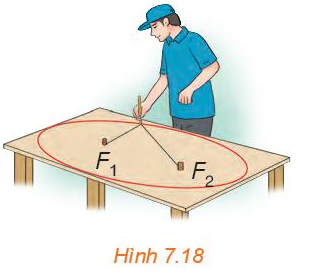
a) Đường vừa nhận được có liên hệ với hình ảnh nào ở Hình 7.17?

b) Trong quá trình đầu bút di chuyển để vẽ nên đường nói trên, tổng các khoảng cách từ nó tới các vị trí F₁, F₂ có thay đổi không? Vì sao?

Xét một elip (E) với các kí hiệu như trong định nghĩa. Chọn hệ trục tọa độ Oxy có gốc O là trung điểm của F₁F₂, tia Ox trùng tia OF₂ (H.7.21). 

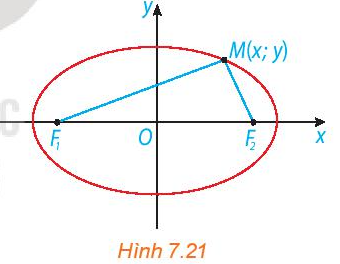
a) Nêu tọa độ của các tiêu điểm F₁, F₂.

b) Giải thích vì sao điểm M(x; y) thuộc elip khi và chỉ khi

$\sqrt{{\left(x+c\right)}^2+y^2} + \sqrt{{\left(x-c\right)}^2+y^2}=2a$.             (1)

Chú ý. Người ta có thể biến đổi (1) về dạng $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$, với $b=\sqrt{a^2-c^2}$.

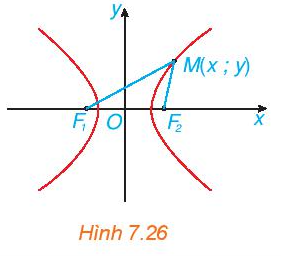
Xét một hypebol (H) với các kí hiệu như trong định nghĩa. Chọn hệ trục tọa độ Oxy có gốc O là trung điểm của F₁F₂, tia Ox trùng tia OF₂ (H.7.26). Nêu tọa độ của các tiêu điểm F₁, F₂. Giải thích vì sao điểm M(x; y) thuộc (H) khi và chỉ khi

$\left|\sqrt{{\left(x+c\right)}^2+y^2}-\sqrt{{\left(x-c\right)}^2+y^2}\right|=2a$. (3)

Cho hypebol (H): $\frac{x^2}{144}-\frac{y^2}{25}=1$. Tìm các tiêu điểm và tiêu cự của (H).

Cho parabol (P): y = 1/4x². Xét F(0; 1) và đường thẳng Δ: y + 1 = 0. Với điểm M(x; y) bất kì, chứng minh rằng MF = d(M, Δ) ⇔ M(x; y) thuộc (P).