Tam thức f(x) = x^2 – 2x – 3 nhận giá trị dương khi và chỉ khi
Câu hỏi:
Tam thức f(x) = x2 – 2x – 3 nhận giá trị dương khi và chỉ khi
A. x ∈ (– ∞; – 3) \( \cup \) (– 1; + ∞);
B. x ∈ (– ∞; – 1) \( \cup \) (3; + ∞);
C. x ∈ (– ∞; – 2) \( \cup \) (6; + ∞);
Trả lời:
Đáp án đúng là: B
Xét f(x) = x2 – 2x – 3 có ∆’ = (–1)2 – 1(–3) = 4 > 0 và a = 1 > 0 nên hàm số có hai nghiệm phân biệt x1 = –1 và x2 = 3.
Khi đó, ta có bảng xét dấu:
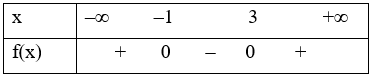
Suy ra f(x) > 0 với x ∈ (– ∞; – 1) \( \cup \) (3; + ∞); f(x) < 0 khi x ∈ (– 1; 3)
Vậy f(x) nhận giá trị dương khi x ∈ (– ∞; – 1) \( \cup \) (3; + ∞).
Xem thêm bài tập trắc nghiệm Toán 10 KNTT có lời giải hay khác:
Câu 1:
Tập xác định của hàm số \[y = \frac{{x - 1}}{{{x^2} - x + 3}}\] là
Xem lời giải »
Câu 2:
Cho hàm số có đồ thị như hình vẽ
Kết luận nào sau đây là đúng
Xem lời giải »
Câu 3:
Tọa độ đỉnh I của parabol (P): y = x2 + 8x + 12 là
Xem lời giải »
Câu 5:
Cho parabol (P): y = ax2 + bx + 1. Xác định (P) biết rằng parabol đi qua hai điểm A(1; 4) và B(– 1; 2).
Xem lời giải »
Câu 6:
Nghiệm của phương trình \[\sqrt {2x - 3} = x - 3\]
Xem lời giải »
Câu 7:
Số nghiệm của phương trình \[\sqrt {{x^2} - 3x} = \sqrt {2x - 4} \]
Xem lời giải »
Câu 8:
Tập xác định của hàm số \[y = \frac{{\sqrt {x - 2} - 2}}{{x - 6}}\] là:
Xem lời giải »


