Giải Toán 10 trang 12 Tập 2 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 12 Tập 2 trong Bài 16: Hàm số bậc hai Toán lớp 10 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 12.

Giải Toán 10 trang 12 Tập 2 Kết nối tri thức

Câu hỏi trang 12 Toán 10 Tập 2: Hàm số nào dưới đây là hàm số bậc hai?

A. y = x⁴ + 3x² + 2.

B. $y=\frac{1}{x^2}$. 

C. y = – 3x²+ 1. 

D. $y=3{\left(\frac{1}{x}\right)}^2+3\frac{1}{x}-1$. 

Lời giải:

Đáp án đúng là: C

Hàm số bậc hai là hàm số cho bởi công thức y = ax²+ bx + x với a, b, c là các hằng số và a ≠ 0. 

Vậy trong các hàm số đã cho thì hàm số y = – 3x² + 1 là hàm số bậc hai với các hệ số a = – 3, b = 0 và c = 1. 

Chú ý: Hàm số $y=3{\left(\frac{1}{x}\right)}^2+3\frac{1}{x}-1$ không phải là hàm số bậc hai, mà đây là hàm số có thể đưa về dạng bậc hai nếu ta đặt $t=\frac{1}{x}$.

Luyện tập 1 trang 12 Toán 10 Tập 2: Cho hàm số y = (x – 1)(2 – 3x). 

a) Hàm số đã cho có phải là hàm số bậc hai không? Nếu có, hãy xác định các hệ số a, b, c của nó. 

b) Thay dấu “?” bằng các số thích hợp để hoàn thành bảng giá trị sau của hàm số đã cho. 

x	– 2	– 1	0	1
y	?	?	?	?

 

Lời giải:

a) Ta có: y = (x – 1)(2 – 3x) = 2x – 3x² – 2 + 3x = – 3x² + 5x – 2.

Suy ra y = – 3x² + 5x – 2, đây là hàm số bậc hai với các hệ số a = – 3, b = 5, c = – 2. 

b) Với x = – 2 thì y = – 3 . (– 2)² + 5 . (– 2) – 2 = – 24.

Với x = – 1 thì y = – 3 . (– 1)² + 5 . (– 1) – 2 = – 10.

Với x = 0 thì y = – 3 . 0² + 5 . 0 – 2 = – 2.

Với x = 1 thì y = – 3 . 1² + 5 . 1 – 2 = 0. 

Vậy ta có bảng sau: 

x	– 2	– 1	0	1
y	– 24	– 10	– 2	0

 

Vận dụng 1 trang 12 Toán 10 Tập 2: Một viên bi rơi tự do từ độ cao 19,6 m xuống mặt đất. Độ cao h (mét) so với mặt đất của viên bi trong khi rơi phụ thuộc vào thời gian t (giây) theo công thức: h = 19,6 – 4,9t²; h, t ≥ 0. 

a) Hỏi sau bao nhiêu giây kể từ khi rơi thì viên bi chạm đất?

b) Tìm tập xác định và tập giá trị của hàm số h. 

Lời giải:

a) Viên bi rơi chạm đất thì h = 0. 

Khi đó: 19,6 – 4,9t²= 0 ⇔ 4,9t²= 19,6 ⇔ t² = 4 ⇔ t = 2 hoặc t = – 2. 

Vì t ≥ 0 nên ta chọn t = 2. 

Vậy sau 2 giây kể từ khi rơi thì viên bi chạm đất. 

b) Ta có: h = 19,6 – 4,9t²

Đây là hàm số bậc hai với biến t, mà t ≥ 0.

Do đó, tập xác định của hàm số h này là D = [0; + ∞). 

Vì t² ≥ 0 với mọi t nên – 4,9t² ≤ 0 với mọi t.

Suy ra – 4,9t²­+ 19,6 ≤ 0 + 19,6 hay 19,6 – 4,9t² ≤ 19,6 với mọi t. 

Do đó: h ≤ 19,6 với mọi t. 

Mặt khác, h ≥ 0.

Khi đó: 0 ≤ h ≤ 19,6 với mọi t. 

Vậy tập giá trị của hàm số h là [0; 19,6]. 

HĐ2 trang 12 Toán 10 Tập 2: Xét hàm số y = S(x) = – 2x² + 20x (0 < x < 10). 

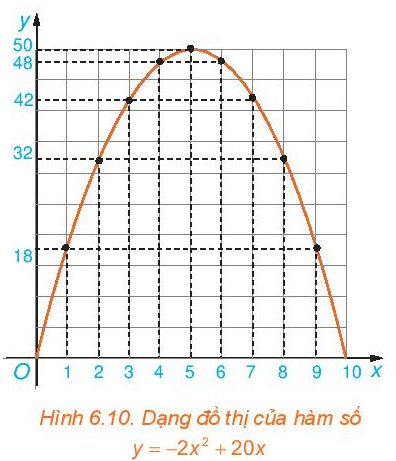
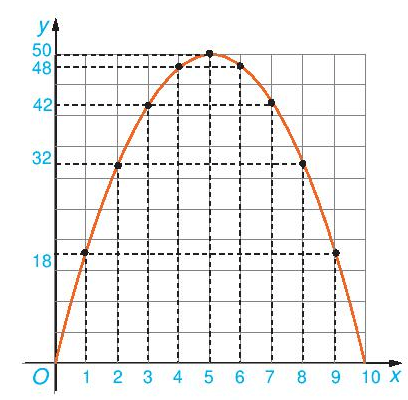
a) Trên mặt phẳng tọa độ Oxy, biểu diễn tọa độ các điểm trong bảng giá trị của hàm số lập được ở Ví dụ 1. Nối các điểm đã vẽ lại ta được dạng đồ thị hàm số y = – 2x² + 20x trên khoảng (0; 10) như trong Hình 6.10. Dạng đồ thị của hàm số y = – 2x² + 20x có giống với đồ thị của hàm só y = – 2x² hay không?

b) Quan sát dạng đồ thị của hàm số y = – 2x² + 20x trong Hình 6.10, tìm tọa độ điểm cao nhất của đồ thị. 

c) Thực hiện phép biến đổi 

y = – 2x² + 20x = – 2(x² – 10x) = – 2(x² – 2 . 5 . x + 25) + 50 = – 2(x – 5)² + 50. 

Hãy cho biết giá trị lớn nhất của diện tích mảnh đất được rào chắn. Từ đó suy ra lời giải của bài toán ở phần mở đầu. 

Lời giải:

a) Ta biểu diễn các điểm có tọa độ (0; 0), (2; 32), (4; 48), (5; 50), (6; 48), (8; 32), (10; 0) lên mặt phẳng tọa độ và nối lại, ta được dạng của đồ thị hàm số y = – 2x² + 20x trên khoảng (0; 10). 

Dạng của đồ thị hàm số y = – 2x² + 20x giống với dạng của đồ thị hàm số y = – 2x². 

b) Quan sát đồ thị ta thấy tọa độ điểm cao nhất của đồ thị hàm số y = – 2x² + 20x là điểm (5; 50). 

c) Vì (x – 5)² ≥ 0 với mọi số thực x 

Suy ra – 2(x – 5)² ≤ 0 với mọi số thực x

Do đó: – 2(x – 5)² + 50 ≤ 0 + 50 = 50 với mọi số thực x. 

Khi đó: y ≤ 50. Vậy giá trị lớn nhất của y là 50 hay diện tích lớn nhất của mảnh đất được rào chắn là 50 m². 

Lời giải bài toán mở đầu: 

Gọi x (mét, x > 0) là khoảng cách từ điểm cọc P và Q đến bờ tường. 

Tấm lưới dài 20 m và được rào chắn ba mặt áp lên bờ tường như Hình 6.8, do đó ta có: 

 x + x + PQ = 20. 

Suy ra: PQ = 20 – x – x = 20 – 2x (m). 

Vì PQ > 0 (độ dài dương) nên 20 – 2x > 0 ⇔ 2x < 20 ⇔ x < 10. 

Do đó ta có điều kiện của x là 0 < x < 10. 

Mảnh đất được rào chắn có dạng hình chữ nhật với hai kích thước là x (m) và 20 – 2x (m) với 0 < x < 10. 

Khi đó diện tích của mảnh đất là S(x) = x . (20 – 2x) = – 2x² + 20x. 

Theo yêu cầu bài toán, ta cần tìm giá trị của x để S(x) có giá trị lớn nhất. 

Ta có: S(x) = – 2(x² – 10x) = – 2(x² – 2 . 5 . x + 25) + 50 = – 2(x – 5)² + 50 ≤ 50 với mọi số thực x. 

Dấu “=” xảy ra khi x – 5 = 0 ⇔ x = 5 (thỏa mãn điều kiện 0 < x < 10). 

Do đó giá trị lớn nhất của S(x) là 50 tại x = 5. 

Vậy hai cột góc hàng rào cần phải cắm cách bờ tường 5 m để mảnh đất được rào chắn của bác Việt có diện tích lớn nhất. 

Lời giải bài tập Toán lớp 10 Bài 16: Hàm số bậc hai Kết nối tri thức hay khác:

• Giải Toán 10 trang 11

• Giải Toán 10 trang 13

• Giải Toán 10 trang 15

• Giải Toán 10 trang 16