Giải Toán 10 trang 26 Tập 1 Kết nối tri thức
Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 26 Tập 1 trong Bài 4: Hệ bất phương trình bậc nhất hai ẩn Toán lớp 10 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 26.
Giải Toán 10 trang 26 Tập 1 Kết nối tri thức
Mở đầu trang 26 Toán 10 Tập 1: Trong năm nay, một cửa hàng điện lạnh dự định kinh doanh hai loại máy điều hòa: điều hòa hai chiều và điều hòa một chiều với số vốn ban đầu không vượt quá 1,2 tỉ đồng.
Cửa hàng ước tính rằng tổng nhu cầu của thị trường sẽ không vượt quá 100 máy cả hai loại. Nếu là chủ cửa hàng thì em cần đầu tư kinh doanh mỗi loại bao nhiêu máy để lợi nhuận thu được là lớn nhất?
Lời giải:
Sau bài học này ta sẽ giải được bài toán như sau:
Gọi x, y lần lượt là số máy điều hòa hai chiều và số máy điều hòa một chiều mà chủ cửa hàng đầu tư (x,y ≥ 0)
Vì tổng nhu cầu của thị trường sẽ không vượt quá 100 máy cả hai loại nên ta có bất phương trình: x + y ≤ 100
Số tiền đầu tư là: 20x + 10y (triệu đồng)
Vì số vốn ban đầu không vượt quá 1,2 tỉ đồng nên ta có bất phương trình:
20x + 10y ≤ 1 200
Lợi nhuận dự kiến chủ cửa hàng thu được là: F(x;y) = 3,5x + 2y (triệu đồng)
Bài toán trở thành tìm giá trị x, y thỏa mãn hệ bất phương trình:
(1) để F(x;y) = 3,5x + 2y là lớn nhất.
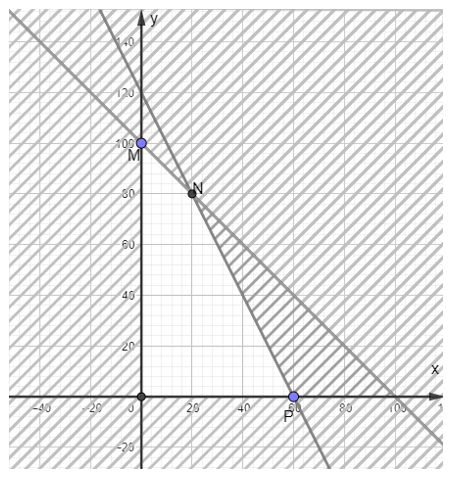
Biểu diễn miền nghiệm của hệ bất phương trình (1) trên mặt phẳng tọa độ bằng cách biểu diễn từng miền nghiệm của từng bất phương trình trong hệ phương trình (1), rồi lấy giao của các miền nghiệm ta được miền nghiệm của hệ BPT (1) là miền tứ giác OMNP với tọa độ các điểm O(0; 0), M(0; 100), N(20; 80), P(60; 0).
Tại O(0;0) giá trị biểu thức F(x;y) = 3,5x + 2y là: 3,5.0 + 2.0 = 0;
Tại M(0;100) giá trị biểu thức 3,5x + 2y là: 3,5.0 + 2.100 = 200;
Tại N(20;80) giá trị biểu thức 3,5x + 2y là: 3,5.20 + 2.80 = 230;
Tại P(60;0) giá trị biểu thức 3,5x + 2y là: 3,5.60 + 2.0 = 210;
Suy ra tại x = 20, y = 80 thì giá trị biểu thức 3,5x + 2y là lớn nhất.
Vậy nếu là chủ cửa hàng thì em cần đầu tư kinh doanh 20 máy điều hòa hai chiều, 80 máy điều hòa một chiều để lợi nhuận thu được là lớn nhất.
HĐ1 trang 26 Toán 10 Tập 1: Trong tình huống mở đầu, gọi x và y lần lượt là số máy điều hòa hai chiều và một chiều mà cửa hàng cần nhập. Tính số tiền vốn cửa hàng phải bỏ ra để nhập hai loại máy điều hòa theo x và y.
a) Do nhu cầu của thị trường không quá 100 máy nên x và y cần thỏa mãn điều kiện gì?
b) Vì số vốn mà chủ cửa hàng có thể đầu tư không vượt quá 1,2 tỉ đồng nên x và y phải thỏa mãn điều kiện gì?
c) Tính số tiền lãi mà chủ cửa hàng dự kiến thu được theo x và y.
Lời giải:
Do x và y là số máy điều hòa mà cửa hàng cần nhập nên x ≥ 0, y ≥ 0.
Số tiền vốn mà chủ cửa hàng phải bỏ ra để nhập hai loại máy điều hòa theo x và y là:
20x + 10y (triệu đồng)
a) Do nhu cầu của thị trường không quá 100 máy nên x + y ≤ 100.
b) Vì số vốn mà chủ cửa hàng có thể đầu tư không vượt quá 1,2 tỉ đồng nên 20x + 10y ≤ 1 200 .
c) Số tiền lãi mà cửa hàng dự kiến thu được là: 3,5x + 2y (triệu đồng).
Lời giải bài tập Toán lớp 10 Bài 4: Hệ bất phương trình bậc nhất hai ẩn Kết nối tri thức hay khác: