Giải Toán 10 trang 34 Tập 2 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 34 Tập 2 trong Bài 19: Phương trình đường thẳng Toán lớp 10 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 34.

Giải Toán 10 trang 34 Tập 2 Kết nối tri thức

Vận dụng trang 34 Toán 10 Tập 2: Việc quy đổi nhiệt độ giữa đơn vị độ C (Anders Celsius, 1701 – 1744) và đơn vị độ F (Daniel Fahrenheit, 1686 – 1736) được xác định bởi hai mốc sau: 

Nước đóng băng ở 0 °C, 32 °F; 

Nước sôi ở 100 °C, 212 °F. 

Trong quy đổi đó, nếu a °C tương ứng với b °F thì trên mặt phẳng tọa độ Oxy, điểm M(a; b) thuộc đường thẳng đi qua A(0; 32) và B(100; 212). 

Hỏi 0 °F, 100 °F tương ứng với bao nhiêu độ C?

Lời giải:

Ta lập phương trình đường thẳng đi qua hai điểm A(0; 32) và B(100; 212). 

Ta có: $\overrightarrow{AB}=\left(100-0;212-32\right)=\left(100;180\right)$.

Chọn $\overrightarrow{u}=\frac{1}{20}\overrightarrow{AB}=\left(5;9\right)$ là một vectơ chỉ phương của AB thì đường thẳng AB có một vectơ pháp tuyến là $\overrightarrow{n}\left(9;-5\right)$. 

Do đó phương trình tổng quát của đường thẳng AB là 

9(x – 0) – 5(y – 32) = 0 hay 9x – 5y + 160 = 0. 

Để tìm 0 °F, 100 °F tương ứng với bao nhiêu độ C nghĩa là ta tìm hoành độ của các điểm thuộc đường thẳng AB có tung độ lần lượt là 0 và 100. 

Tại 0 °F, nghĩa là y = 0 thì 9x – 5 . 0 + 160 = 0 ⇔ 9x = – 160 ⇔ x = $-\frac{160}{9}$.

Tại 100 °F, nghĩa là y = 100 thì 9x – 5 . 100 + 160 = 0 ⇔ 9x = 340 ⇔ x = $\frac{340}{9}$. 

Vậy 0 °F tương ứng với $-\frac{160}{9}$°C và 100 °F tương ứng với $\frac{340}{9}$°C. 

Bài 7.1 trang 34 Toán 10 Tập 2: Trong mặt phẳng tọa độ, cho $\overrightarrow{n}=\left(2;1\right),\overrightarrow{v}=\left(3;2\right),A\left(1;3\right),B\left(-2;1\right)$. 

a) Lập phương trình tổng quát của đường thẳng ∆₁ đi qua A và có vectơ pháp tuyến $\overrightarrow{n}$. 

b) Lập phương trình tham số của đường thẳng ∆₂ đi qua B và có vectơ chỉ phương $\overrightarrow{v}$. 

c) Lập phương trình tham số của đường thẳng AB. 

Lời giải:

a) Đường thẳng ∆₁ đi qua A(1; 3) và có vectơ pháp tuyến $\overrightarrow{n}=\left(2;1\right)$, do đó phương trình tổng quát của ∆₁ là: 2(x – 1) + 1(y – 3) = 0 hay 2x + y – 5 = 0. 

b) Đường thẳng ∆₂ đi qua B(– 2; 1) và có vectơ chỉ phương $\overrightarrow{v}=\left(3;2\right)$, do đó phương trình tham số của ∆₂ là $\left\{\begin{array}{l}x=-2+3t\\ y=1+2t\end{array}\right.$. 

c) Đường thẳng AB đi qua điểm A(1; 3) và nhận $\overrightarrow{AB}=\left(-2-1;1-3\right)=\left(-3;-2\right)$ làm vectơ chỉ phương nên phương trình tham số của đường thẳng AB là $\left\{\begin{array}{l}x=1-3t\\ y=3-2t\end{array}\right.$. 

Bài 7.2 trang 34 Toán 10 Tập 2: Lập phương trình đường thẳng tổng quát của các trục tọa độ. 

Lời giải:

Các vectơ đơn vị của trục Ox và Oy lần lượt là $\overrightarrow{i}\left(1;0\right)$ và $\overrightarrow{j}\left(0;1\right)$. Mỗi vectơ đơn vị chính là 1 vectơ chỉ phương của mỗi trục.

Hai trục tọa độ vuông góc với nhau nên vectơ $\overrightarrow{j}\left(0;1\right)$ chỉ phương của trục này là vectơ pháp tuyến của trục kia. 

Trục Ox đi qua điểm gốc tọa độ O(0; 0) và nhận vectơ làm vectơ pháp tuyến nên phương trình tổng quát của Ox là: 0(x – 0) + 1(y – 0) = 0 hay y = 0. 

Trục Oy đi qua điểm gốc tọa độ O(0; 0) và nhận vectơ $\overrightarrow{i}\left(1;0\right)$ làm vectơ pháp tuyến nên phương trình tổng quát của Oy là: 1(x – 0) + 0(y – 0) = 0 hay x = 0. 

Bài 7.3 trang 34 Toán 10 Tập 2: Cho hai đường thẳng ∆₁:$\left\{\begin{array}{l}x=1+2t\\ y=3+5t\end{array}\right.$ và ∆₂: 2x + 3y – 5 = 0. 

a) Lập phương trình tổng quát của ∆₁. 

b) lập phương trình tham số của ∆₂. 

Lời giải:

a) Đường thẳng ∆₁ có phương trình tham số là $\left\{\begin{array}{l}x=1+2t\\ y=3+5t\end{array}\right.$, do đó đường thẳng ∆­₁ đi qua điểm A(1; 3) và có một vectơ chỉ phương là ${\overrightarrow{u}}_1=\left(2;5\right)$. 

Suy ra một vectơ pháp tuyến của đường thẳng ∆₁ là ${\overrightarrow{n}}_1=\left(5;-2\right)$. 

Do đó phương trình tổng quát của đường thẳng ∆₁ là 5(x – 1) – 2(y – 3) = 0 hay 5x – 2y + 1 = 0. 

b) Đường thẳng ∆₂ có phương trình tổng quát là 2x + 3y – 5 = 0 nên ∆₂ có một vectơ pháp tuyến là ${\overrightarrow{n}}_2=\left(2;3\right)$. 

Suy ra một vectơ chỉ phương của đường thẳng ∆₂ là ${\overrightarrow{u}}_2=\left(3;-2\right)$. 

Ta lấy điểm B(1; 1) thuộc ∆₂ (do 2 . 1 + 3 . 1 – 5 = 0). 

Khi đó đường thẳng ∆₂ đi qua điểm B(1; 1) và nhận ${\overrightarrow{u}}_2=\left(3;-2\right)$ làm vectơ chỉ phương nên phương trình tham số của ∆₂ là $\left\{\begin{array}{l}x=1+3t\\ y=1-2t\end{array}\right.$. 

Bài 7.4 trang 34 Toán 10 Tập 2: Trong mặt phẳng tọa độ, cho tam giác ABC có A(1; 2), B(3; 0) và C(– 2; – 1). 

a) Lập phương trình đường cao kẻ từ A. 

b) Lập phương trình đường trung tuyến kẻ từ B. 

Lời giải:

a) Ta có: $\overrightarrow{BC}=\left(-2-3;-1-0\right)=\left(-5;-1\right)$.

Gọi đường cao kẻ từ đỉnh A của tam giác ABC là đường thẳng ∆, do đó ∆ ⊥ BC. 

Suy ra đường thẳng ∆ đi qua điểm A(1; 2) và nhận vectơ $\overrightarrow{BC}$ làm vectơ pháp tuyến.

Vậy phương trình đường thẳng ∆ là – 5(x – 1) – 1(y – 2) = 0 hay 5x + y – 7 = 0. 

b) Gọi M là trung điểm của AC, khi đó tọa độ của điểm M là 

$\left\{\begin{array}{l}{x}_M=\frac{x_A+x_C}{2}=\frac{1+\left(-2\right)}{2}=\frac{-1}{2}\\ y_M=\frac{y_A+y_C}{2}=\frac{2+\left(-1\right)}{2}=\frac{1}{2}\end{array}\right.$

Hay M$\left(-\frac{1}{2};\frac{1}{2}\right)$

Đường trung tuyến kẻ từ B chính là đường thẳng BM. 

Ta có:$\overrightarrow{BM}=\left(-\frac{1}{2}-3;\frac{1}{2}-0\right)=\left(-\frac{7}{2};\frac{1}{2}\right)$. 

Chọn $\overrightarrow{u}=2\overrightarrow{BM}=\left(-7;1\right)$. 

Đường trung tuyến BM đi qua B(3; 0) và có một vectơ chỉ phương $\overrightarrow{u}=\left(-7;1\right)$, do đó phương trình tham số của đường thẳng BM là $\left\{\begin{array}{l}x=3-7t\\ y=t\end{array}\right.$. 

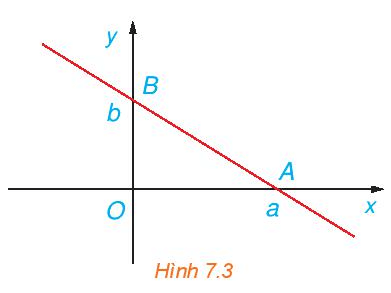
Bài 7.5 trang 34 Toán 10 Tập 2: (Phương trình đoạn chắn của đường thẳng) 

Chứng minh rằng, đường thẳng đi qua hai điểm A(a; 0), B(0; b) với ab ≠ 0 (H.7.3) có phương trình là $\frac{x}{a}+\frac{y}{b}=1$. 

Lời giải:

Ta có: $\overrightarrow{AB}=\left(0-a;b-0\right)=\left(-a;b\right)$. 

Suy ra đường thẳng AB có một vectơ chỉ phương là $\overrightarrow{AB}=\left(-a;b\right)$ nên nó có một vectơ pháp tuyến là $\overrightarrow{n}=\left(b;a\right)$. 

Do đó phương trình tổng quát của đường thẳng AB đi qua điểm A và nhận $\overrightarrow{n}$ làm vectơ pháp tuyến là: b(x – a) + a(y – 0) = 0 hay bx + ay – ab = 0   (1). 

Do ab ≠ 0 nên ta chia cả hai vế của (1) cho ab, ta được: 

$\frac{bx}{ab}+\frac{ay}{ab}-\frac{ab}{ab}=\frac{0}{ab}$

$\iff \frac{x}{a}+\frac{y}{b}-1=0$

. $\iff \frac{x}{a}+\frac{y}{b}=1$

Vậy đường thẳng đi qua hai điểm A(a; 0), B(0; b) với ab ≠ 0 có phương trình là $\frac{x}{a}+\frac{y}{b}=1$.

Bài 7.6 trang 34 Toán 10 Tập 2: Theo Google Maps, sân bay Nội Bài có vĩ độ 21,2° Bắc, kinh độ 105,8° Đông, sân bay Đà Nẵng có vĩ độ 16,1° Bắc, kinh độ 108,2° Đông. Một máy bay, bay từ sân bay Nội Bài đến sân bay Đà Nẵng. Tại thời điểm t giờ, tính từ lúc xuất phát, máy bay ở vị trí đó có vĩ độ x° Bắc, kinh độ y° Đông được tính theo công thức

 $\left\{\begin{array}{l}x=\mathrm{21,2}-\frac{153}{40}t\\ y=\mathrm{105,8}+\frac{9}{5}t\end{array}\right.$

a) Hỏi chuyến bay từ Hà Nội đến Đà Nẵng mất mấy giờ?

b) Tại thời điểm 1 giờ kể từ lúc cất cánh, máy bay đã bay qua vĩ tuyến 17 (17° Bắc) chưa? 

Lời giải:

a) Tại sân bay Nội Bài, máy bay bắt đầu bay ứng với thời gian t = 0. 

Tọa độ của sân bay Đà Nẵng thỏa mãn hệ $\left\{\begin{array}{l}x=\mathrm{21,2}-\frac{153}{40}t\\ y=\mathrm{105,8}+\frac{9}{5}t\end{array}\right.$. 

Do đó, thời gian máy bay bay từ Hà Nội đến Đà Nẵng là nghiệm t của hệ $\left\{\begin{array}{l}\mathrm{16,1}=\mathrm{21,2}-\frac{153}{40}t\left(1\right)\\ \mathrm{108,2}=\mathrm{105,8}+\frac{9}{5}t\left(2\right)\end{array}\right.$.

Từ (1) suy ra t = $\frac{4}{3}$. 

Từ (2) suy ra t = $\frac{4}{3}$. 

Do đó t = $\frac{4}{3}$ là nghiệm của hệ trên. 

Vậy chuyến bay từ Hà Nội đến Đà Nẵng mất $\frac{4}{3}$ giờ. 

b) Tại thời điểm 1 giờ kể từ lúc cất cánh, nghĩa là t = 1, thay vào hệ $\left\{\begin{array}{l}x=\mathrm{21,2}-\frac{153}{40}t\\ y=\mathrm{105,8}+\frac{9}{5}t\end{array}\right.$ ta được: $\left\{\begin{array}{l}x=\mathrm{21,2}-\frac{153}{40}.1\\ y=\mathrm{105,8}+\frac{9}{5}.1\end{array}\right.\iff \left\{\begin{array}{l}x=\mathrm{17,375}\\ y=\mathrm{107,6}\end{array}\right.$. 

Do đó tại thời điểm 1 giờ kể từ lúc cất cánh, máy bay đang ở vị trí có 17,375° Bắc và có kinh độ 107,6° Đông. 

Vậy tại thời điểm 1 giờ kể từ lúc cất cánh, máy bay đã bay qua vĩ tuyến 17 (17° Bắc).

Lời giải bài tập Toán lớp 10 Bài 19: Phương trình đường thẳng Kết nối tri thức hay khác:

• Giải Toán 10 trang 31

• Giải Toán 10 trang 32

• Giải Toán 10 trang 33