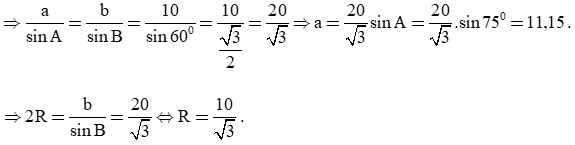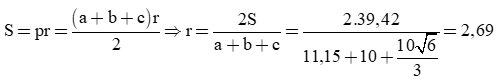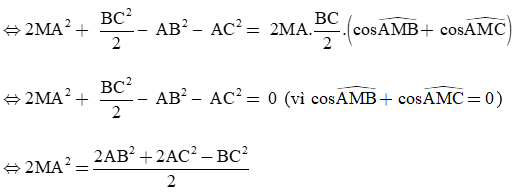Giải Toán 10 trang 44 Tập 1 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 44 Tập 1 trong Bài tập cuối chương III Toán lớp 10 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 44.

Giải Toán 10 trang 44 Tập 1 Kết nối tri thức

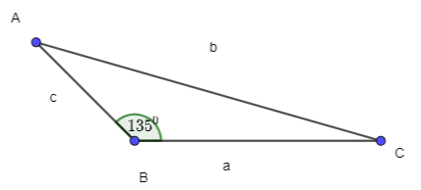
Bài 3.12 trang 44 Toán 10 Tập 1: Cho tam giác ABC có $\widehat{B}={135}^0$. Khẳng định nào sau đây là đúng?

a)

A. $S=\frac{1}{2}ca.$           

B. $S=\frac{-\sqrt{2}}{4}ac.$  

C. $S=\frac{\sqrt{2}}{4}bc.$

D. $S=\frac{\sqrt{2}}{4}ca.$

b)

A. $R=\frac{a}{\sin A}.$

B. $R=\frac{\sqrt{2}}{2}b.$

C. $R=\frac{\sqrt{2}}{2}c.$

D. $R=\frac{\sqrt{2}}{2}a.$

c)

A. $a^2=b^2+c^2+\sqrt{2}ab$.

B. $\frac{b}{\sin A}=\frac{a}{\sin B}.$

C. $\sin B=\frac{-\sqrt{2}}{2}.$

D. b² = c² + a² – 2ca.cos135⁰.

Lời giải:

a) Diện tích tam giác ABC:

$S=\frac{1}{2}.a.c.\sin B=\frac{1}{2}a.c.\sin {135}^0=\frac{\sqrt{2}}{4}ac$.

Chọn D.

b) Ta có:

$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$ (định lí sin)

$\Rightarrow R=\frac{b}{2\sin B}=\frac{b}{2\sin {135}^0}=\frac{b}{\sqrt{2}}=\frac{\sqrt{2}}{2}b.$

Chọn B.

c) Theo định lí cos, ta có:

b² = a² + c² – 2ac.cosB = a² + c² – 2ac.cos135⁰.

Chọn D.

Bài 3.13 trang 44 Toán 10 Tập 1: Cho tam giác ABC. Khẳng định nào sau đây là đúng?

a)

A. $S=\frac{abc}{4r}.$

B. $r=\frac{2S}{a+b+c}.$

C. a² = b² + c² + 2bc.cosA.

D. S = r(a + b + c).

b)

A. sinA = sin(B + C).

B. cosA = cos(B + C).

C. cosA > 0.

D. sinA ≤ 0

Lời giải:

a) Ta có:

$S=pr=\frac{abc}{4R}=\frac{\left(a+b+c\right)r}{2}$.

Do đó A,D sai.

Theo định lí cos, ta có: a² = b² + c² - 2bc.cosA. Do đó C sai.

Ta có:

$S=\frac{\left(a+b+c\right)r}{2}\Rightarrow r=\frac{2S}{a+b+c}$.

Do đó B đúng.

Chọn B

b) Ta có: 

$\widehat{A}+\widehat{B}+\widehat{C}={180}^0\Rightarrow \widehat{A}={180}^0-\left(\widehat{B}+\widehat{C}\right)$

$\sin \widehat{A}=\sin \left[{180}^0-\left(\widehat{B}+\widehat{C}\right)\right]=\sin \left(\widehat{B}+\widehat{C}\right)$. Do đó A đúng.

$co\mathrm{s}\widehat{A}=co\mathrm{s}\left[{180}^0-\left(\widehat{B}+\widehat{C}\right)\right]=-co\mathrm{s}\left(\widehat{B}+\widehat{C}\right)$. Do đó B sai.

Ta có: cosA > 0 khi 0⁰ < $\widehat{A}$ < 90⁰, mà góc A có thể là góc tù hay $\widehat{A}>90°$. Do đó C sai.

Trong một tam giác, ta có: $0^0\le \widehat{A}\le {180}^0$ ⇒ sin A > 0. Do đó D sai.

Chọn A

Bài 3.14 trang 44 Toán 10 Tập 1: Tính giá trị các biểu thức sau:

a) M = sin45⁰.cos45⁰ + sin30⁰;

b) $\text{}N=\sin {60}^0.cos{30}^0+\frac{1}{2}\sin {45}^0.cos{45}^0$;

c) P = 1 + tan²60⁰;

d) $Q=\frac{1}{{\sin }^{2}120°}-{\cot }^{2}120°.$

Lời giải:

a) M = sin45⁰.cos45⁰ + sin30⁰

$=\frac{\sqrt{2}}{2}.\frac{\sqrt{2}}{2}+\frac{1}{2}=\frac{1}{2}+\frac{1}{2}=1$

b) 

$\text{}N=\sin {60}^0.cos{30}^0+\frac{1}{2}\sin {45}^0.cos{45}^0$

= $\frac{\sqrt{3}}{2}.\frac{\sqrt{3}}{2}+\frac{1}{2}.\frac{\sqrt{2}}{2}.\frac{\sqrt{2}}{2}=\frac{3}{4}+\frac{1}{4}=1$

c) P = 1 + tan²60⁰

$=1+{\left(\sqrt{3}\right)}^2=1+3=4$

d) $Q=\frac{1}{{\sin }^{2}120°}-{\cot }^{2}120°.$       

Cách 1: Ta có $\frac{1}{{\sin }^{2}120°}=1+{\cot }^{2}120°$

Do đó $Q=\left(1+{\cot }^{2}120°\right)-{\cot }^{2}120°$ = 1.

Cách 2: $\sin 120°=\frac{\sqrt{3}}{2}$; $\cot 120°=\frac{-1}{\sqrt{3}}$

Thay vào Q, ta được:

Q $=\frac{1}{{\left(\frac{\sqrt{3}}{2}\right)}^2}-{\left(\frac{-1}{\sqrt{3}}\right)}^2$ $=\frac{1}{\frac{3}{4}}-\frac{1}{3}=\frac{4}{3}-\frac{1}{3}=1$.

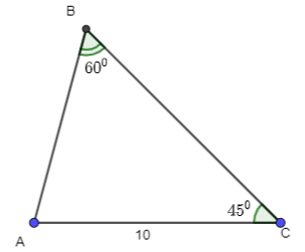
Bài 3.15 trang 44 Toán 10 Tập 1: Cho tam giác ABC có $\widehat{B}={60}^0,\widehat{C}={45}^0,$ AC = 10. Tính a, R, S, r.

Lời giải:

Xét ΔABC, có:

Ta có: 

$\widehat{A}={180}^0-\widehat{B}-\widehat{C}=$180⁰ – 60⁰ –  45⁰ = 75⁰

$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$ (định lí sin)

Diện tích tam giác ABC là:

$S=\frac{1}{2}.b.a.\sin C=\frac{1}{2}\mathrm{.10.11},15.\sin {45}^0$ ≈ 39,42 (đvdt)

$$\begin{gathered} \Rightarrow \frac{c}{\sin C}=\frac{b}{\sin B}=\frac{20}{\sqrt{3}} \\ \Rightarrow c=\frac{20}{\sqrt{3}}\sin C=\frac{20}{\sqrt{3}}.\sin {45}^0=\frac{10\sqrt{6}}{3} \end{gathered}$$

Ta có:

Vậy a = 11,15; $R=\frac{10}{\sqrt{3}},c=\frac{10\sqrt{6}}{3},$ r = 2,69.

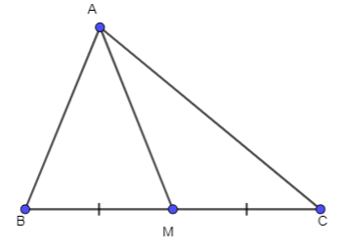
Bài 3.16 trang 44 Toán 10 Tập 1: Cho tam giác ABC có trung tuyến AM. Chứng minh rằng:

a) $cos\widehat{AMB}+cos\widehat{AMC}=0;$

b) MA² + MB² – AB² = 2MA.MB.cos$\widehat{AMB}$ và MA² + MC² – AC² = 2MA.MC.cos$\widehat{AMC}$;

c) $M{A}^2=\frac{2\left(A{B}^2+A{C}^2\right)-B{C}^2}{4}$ (công thức đường trung tuyến).

Lời giải:

a) $cos\widehat{AMB}+cos\widehat{AMC}=0$

Ta có: $\widehat{AMB}+\widehat{AMC}={180}^0$

$\widehat{AMC}={180}^0-\widehat{AMB}$

$cos\widehat{AMB}=-cos\left({180}^0-\widehat{AMB}\right)=-cos\widehat{AMC}$

$\Rightarrow cos\widehat{AMB}+cos\widehat{AMC}$

$=-cos\widehat{AMC}+cos\widehat{AMC}=0$

b) Xét ΔAMB, ta có:

AB² = MA² + MB² – 2MA.MB.cos$\widehat{AMB}$

⇔ MA² + MB² – AB² = 2MA.MB.cos$\widehat{AMB}$(1)

Xét ΔAMC, ta có:

AC² = MA² + MC² – 2MA.MC.cos$\widehat{AMC}$

⇔ MA² + MC² – AC² = 2MA.MC.cos$\widehat{AMC}$ (2)

c) Cộng vế với vế của (1) với (2), ta được:

MA² + MB² – AB² + MA² + MC² – AC² = 2MA.MB.cos$\widehat{AMB}$ + 2MA.MC.cos$\widehat{AMC}$ 

$\iff 2M{A}^2+\frac{B{C}^2}{4}–A{B}^2+\frac{B{C}^2}{4}–A{C}^2$

$=2MA.\frac{BC}{2}.cos\widehat{AMB} +2MA.\frac{BC}{2}.cos\widehat{AMC}$

(Vì $MB=MC=\frac{BC}{2}$)

$\iff M{A}^2=\frac{2\left(A{B}^2+A{C}^2\right)-B{C}^2}{4}$ (công thức đường trung tuyến).

Bài 3.17 trang 44 Toán 10 Tập 1: Cho tam giác ABC. Chứng minh rằng:

a) Nếu góc A nhọn thì b² + c² > a²;

b) Nếu góc A tù thì b² + c² < a²;

c) Nếu góc A vuông thì b² + c² = a².

Lời giải:

Xét ΔABC, có:

Theo định lí cos, ta có: a² = b² + c² – 2bc.cosA

a) Nếu góc A nhọn thì cosA > 0 ⇒ 2bccosA > 0 ⇒ - 2bccosA < 0

Do đó: a² = b² + c² – 2bc.cosA < b² + c²

Vậy b² + c² > a²

b) Nếu góc A tù thì cosA > 0 ⇒ 2bccosA < 0 ⇒ - 2bccosA > 0

Do đó: a² = b² + c² – 2bc.cosA > b² + c²

Vậy b² + c² < a².

c) Nếu góc A vuông thì cosA = 0 ⇒ 2bccosA = 0

Do đó: a² = b² + c² – 2bc.cosA = b² + c²

Vậy b² + c² = a².

Lời giải bài tập Toán lớp 10 Bài tập cuối chương III Kết nối tri thức hay khác:

• Giải Toán 10 trang 45