Giải Toán 10 trang 50 Tập 2 Kết nối tri thức

Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 50 Tập 2 trong Bài 22: Ba đường conic Toán lớp 10 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 50.

Giải Toán 10 trang 50 Tập 2 Kết nối tri thức

Luyện tập 1 trang 50 Toán 10 Tập 2: Cho elip có phương trình chính tắc $\frac{x^2}{100}+\frac{y^2}{64}=1$. Tìm các tiêu điểm và tiêu cự của elip. 

Lời giải:

Ta có: a² = 100, b² = 64. Do đó c = $\sqrt{a^2-b^2}=\sqrt{100-64}=\sqrt{36}=6$. 

Vậy elip có hai tiêu điểm là F₁(– 6; 0); F₂(6; 0) và tiêu cự là F₁F₂ = 2c = 2 . 6 = 12. 

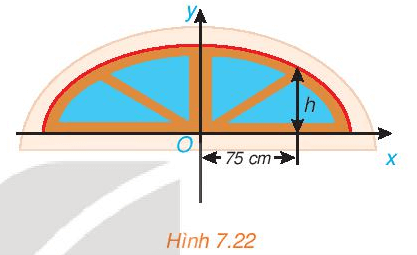
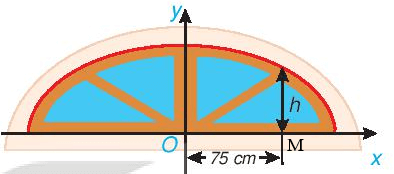
Vận dụng 1 trang 50 Toán 10 Tập 2: Trong bản vẽ thiết kế, vòm của ô thoáng trong Hình 7.22 là nửa nằm phía trên trục hoành của elip có phương trình 

$\frac{x^2}{16}+\frac{y^2}{4}=1$.

Biết rằng 1 đơn vị trên mặt phẳng tọa độ của bản vẽ thiết kế ứng với 30 cm trên thực tế. Tính chiều cao h của ô thoáng tại điểm cách điểm chính giữa của đế ô thoáng 75 cm.

Lời giải:

Ta có 30 cm trên thực tế ứng với 1 đơn vị trên mặt phẳng tọa độ.

Nên 75 cm trên thực tế ứng với 75 : 30 = 2,5 đơn vị trên mặt phẳng tọa độ.

Gọi điểm M trên elip thỏa mãn có hoành độ là 2,5, suy ra tọa độ M(2,5; y)

Mà M thuộc (E) nên tọa độ điểm M thỏa mãn phương trình (E), do đó: 

$\frac{{\left(\mathrm{2,5}\right)}^2}{16}+\frac{y^2}{4}=1\Rightarrow y^2=\frac{39}{16}\Rightarrow y=\frac{\sqrt{39}}{4}\approx \mathrm{1,56}$

Khi đó chiều cao của ô thoáng là: h ≈ 1,56 . 30 = 46,8 cm.

Vậy chiều cao của ô thoáng khoảng 46,8 cm. 

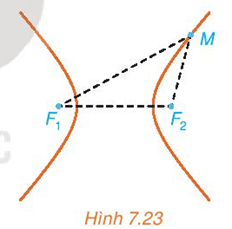
HĐ3 trang 50 Toán 10 Tập 2: Giả sử thiết bị tại F₂ nhận được tín hiệu âm thanh sớm hơn thiết bị tại F₁ là 2 giây và vận tốc âm thanh là 343 m/s. 

a) Tìm mối quan hệ giữa các khoảng cách từ nơi phát ra tín hiệu âm thanh tới F₁, F₂. 

b) Việc giới hạn khu vực tìm kiếm nơi phát ra tín hiệu âm thanh có liên quan đến bài toán tìm tập hợp những điểm M thỏa mãn MF₁ – MF₂ = 686 (m) hay không? 

Lời giải:

a) Giả sử nơi phát ra tín hiệu âm thanh là tại vị trí điểm M. 

Khi đó MF₁ là khoảng cách từ nơi phát ra tín hiệu âm thanh tới F₁ và MF₂ là khoảng cách từ nơi phát ra tín hiệu âm thanh tới F₂.

Gọi t₁ là thời gian âm thanh phát từ M đến F₁, t₂ là thời gian âm thanh phát từ M đến F₂. 

Thiết bị tại F₂ nhận được tín hiệu âm thanh sớm hơn thiết bị tại F₁ là 2 giây nên t₁ – t₂ = 2. 

Vận tốc âm thanh là 343 m/s. 

Khi đó ta có: MF₁ = 343.t₁; MF₂ = 343.t₂. 

Suy ra: MF₁ – MF₂ = 343.t₁ – 343.t₂ = 343.(t₁ – t₂) = 343 . 2 = 686 (m). 

Vậy mối quan hệ giữa các khoảng cách từ nơi phát ra tín hiệu âm thanh tới F₁, F₂ là MF₁ – MF₂ = 686 (m). 

b) Việc giới hạn khu vực tìm kiếm nơi phát ra tín hiệu âm thanh chính là việc giải quyết bài toán tìm tập hợp những điểm M thỏa mãn MF₁ – MF₂ = 686 (m). 

Lời giải bài tập Toán lớp 10 Bài 22: Ba đường conic Kết nối tri thức hay khác:

• Giải Toán 10 trang 48

• Giải Toán 10 trang 49

• Giải Toán 10 trang 51

• Giải Toán 10 trang 52

• Giải Toán 10 trang 53

• Giải Toán 10 trang 56