Giải Toán 10 trang 51 Tập 2 Kết nối tri thức

Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 51 Tập 2 trong Bài 22: Ba đường conic Toán lớp 10 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 51.

Giải Toán 10 trang 51 Tập 2 Kết nối tri thức

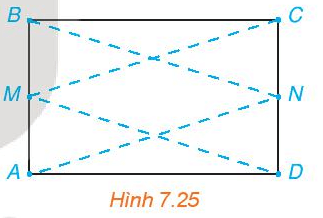
Luyện tập 3 trang 51 Toán 10 Tập 2: Cho hình chữ nhật ABCD và M, N tương ứng là trung điểm của các cạnh AB, CD (H.7.25). Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một hypebol có hai tiêu điểm là M và N.

Lời giải:

Do ABCD là hình chữ nhật nên AB = CD. 

Vì M, N tương ứng là trung điểm của các cạnh AB, CD nên AM = BM = $\frac{1}{2}$AB và CN = DN = $\frac{1}{2}$CD. 

Do đó ta có: BM = CN = AM = DN  (*). 

Khi đó BM // = ND nên BMDN là hình bình hành, suy ra BN = MD (1). 

Tương tự AN = CM (2). 

Hơn nữa ta chứng minh được BMNC là hình chữ nhật nên hai đường chéo BN và MC bằng nhau hay BN = MC (3). 

Từ (1), (2) và (3) suy ra: BN = CM = AN = DM (**).

Từ (*) và (**) ta có: |BN – BM| = |CN – CM| = |AN – AM| = |DN – DM| < MN (bất đẳng thức tam giác).

Vậy A, B, C, D cùng thuộc một hypebol có hai tiêu điểm là M và N.

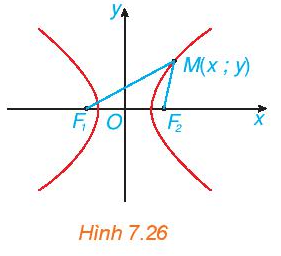
HĐ4 trang 51 Toán 10 Tập 2: Xét một hypebol (H) với các kí hiệu như trong định nghĩa. Chọn hệ trục Oxy có gốc O là trung điểm của F₁F₂, tia Ox trùng tia OF₂ (H.7.26). Nêu tọa độ của các tiêu điểm F₁, F₂. Giải thích vì sao điểm M(x; y) thuộc (H) khi và chỉ khi

$\left|\sqrt{{\left(x+c\right)}^2+y^2}-\sqrt{{\left(x-c\right)}^2+y^2}\right|=2a$. (3)

Lời giải:

+) Vì F₁F₂ = 2c, mà O là trung điểm của F₁F₂. 

Do đó ta có: F₁O = F₂O = 2c : 2 = c. 

Quan sát hình ta thấy, điểm F₁ thuộc trục Ox, nằm bên trái điểm O và cách O một khoảng bằng F₁O nên tọa độ F₁(– c; 0). 

Điểm F₂ thuộc trục Ox, nằm bên phải điểm O và cách O một khoảng bằng F₂O nên tọa độ F₂(c; 0). 

Vậy tọa độ các tiêu điểm: F₁(– c; 0) và F₂(c; 0).

+) Giả sử M(x; y) thuộc hypebol (H) ta cần chứng minh: 

$\left|\sqrt{{\left(x+c\right)}^2+y^2}-\sqrt{{\left(x-c\right)}^2+y^2}\right|=2a$.

Thật vậy, M thuộc hypebol (H) nên: |MF₁ – MF₂|= 2a.

Lại có: MF₁ = $\sqrt{{\left(x-\left(-c\right)\right)}^2+{\left(y-0\right)}^2}=\sqrt{{\left(x+c\right)}^2+y^2}$; 

MF₂ = $\sqrt{{\left(x-c\right)}^2+{\left(y-0\right)}^2}=\sqrt{{\left(x-c\right)}^2+y^2}$.

⇒ |MF₁ – MF₂| = $\left|\sqrt{{\left(x+c\right)}^2+y^2}-\sqrt{{\left(x-c\right)}^2+y^2}\right|=2a$.

Vậy $\left|\sqrt{{\left(x+c\right)}^2+y^2}+\sqrt{{\left(x-c\right)}^2+y^2}\right|=2a$.

+) Giả sử $\left|\sqrt{{\left(x+c\right)}^2+y^2}-\sqrt{{\left(x-c\right)}^2+y^2}\right|=2a$, ta cần chứng minh M thuộc hypebol (H). 

Thật vậy: $\left|\sqrt{{\left(x+c\right)}^2+y^2}-\sqrt{{\left(x-c\right)}^2+y^2}\right|=2a$ nên: |MF₁ – MF₂|= 2a.

Vậy M thuộc hypebol (H).

Lời giải bài tập Toán lớp 10 Bài 22: Ba đường conic Kết nối tri thức hay khác:

• Giải Toán 10 trang 48

• Giải Toán 10 trang 49

• Giải Toán 10 trang 50

• Giải Toán 10 trang 52

• Giải Toán 10 trang 53

• Giải Toán 10 trang 56