Giải Toán 10 trang 72 Tập 1 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm với giải Toán 10 trang 72 Tập 1 trong Bài tập cuối chương IV Toán lớp 10 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10 trang 72.

Giải Toán 10 trang 72 Tập 1 Kết nối tri thức

Bài 4.34 trang 72 Toán 10 Tập 1: Cho hình bình hành ABCD. Chứng minh rằng với mọi điểm M, ta có:

$\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{MD}$

Lời giải:

Gọi O là giao điểm của AC và BD. Khi đó O là trung điểm của AC và O cũng là trung điểm của BD.

$$\begin{gathered} VT=\overrightarrow{MA}+\overrightarrow{MC} \\ =\overrightarrow{MO}+\overrightarrow{OA}+\overrightarrow{MO}+\overrightarrow{OC}=2\overrightarrow{MO}; \end{gathered}$$

$$\begin{gathered} VP=\overrightarrow{MB}+\overrightarrow{MD} \\ =\overrightarrow{MO}+\overrightarrow{OB}+\overrightarrow{MO}+\overrightarrow{OD}=2\overrightarrow{MO}; \end{gathered}$$

$\Rightarrow VT=VP$

Bài 4.35 trang 72 Toán 10 Tập 1: Trong mặt phẳng tọa độ Oxy, cho A(2;1), B(-2;5) và C(-5;2).

a) Tìm tọa độ của các vecto $\overrightarrow{BA}$ và $\overrightarrow{BC}.$

b) Chứng minh rằng A, B, C là ba đỉnh của một tam giác vuông. Tính diện tích và chu vi của tam giác đó.

c) Tìm tọa độ trọng tâm G của tam giác ABC.

d) Tìm tọa độ của điểm D sao cho tứ giác BCAD là một hình bình hành.

Lời giải:

a) Ta có: $\overrightarrow{BA}\left(4;-4\right)$ và $\overrightarrow{BC}\left(-3;-3\right).$

b) Ta có: $\overrightarrow{BA}.\overrightarrow{BC}$ = 4.(–3) + (–4).(–3) = –12 + 12 = 0

⇒ BA ⊥ BC

∆ABC vuông tại B.

Diện tích tam giác vuông ABC là:

$S_{\Delta ABC}=\frac{1}{2}.AB.BC$

$=\frac{1}{2}.\sqrt{4^2+{\left(-4\right)}^2}.\sqrt{{\left(-3\right)}^2+{\left(-3\right)}^2}$

$=\frac{1}{2}.4\sqrt{2}.3\sqrt{2}=12$ (đvdt)

c) Tọa độ trọng tâm G của tam giác ABC là:

$\left\{\begin{array}{l}{x}_G=\frac{2+\left(-2\right)+\left(-5\right)}{3}=\frac{-5}{3}\\ y_G=\frac{1+5+2}{3}=\frac{8}{3}\end{array}\right.$

$\Rightarrow G\left(\frac{-5}{3};\frac{8}{3}\right)$

Vậy tọa độ trọng tâm của tam giác ABC là: $G\left(\frac{-5}{3};\frac{8}{3}\right).$

d) Để tứ giác BCAD là hình bình hành khi $\overrightarrow{DA}=\overrightarrow{BC}$

Ta có: $\overrightarrow{DA}\left(2-x;1-y\right)$ và $\overrightarrow{BC}\left(-3;-3\right)$

Khi đó, ta có hệ phương trình:

$\left\{\begin{array}{l}2-x=-3\\ 1-y=-3\end{array}\right.\iff \left\{\begin{array}{l}x=5\\ y=4\end{array}\right.\Rightarrow D\left(5;4\right)$.

Vậy với D(5;4) thì tứ giác BCAD là một hình bình hành.

Bài 4.36 trang 72 Toán 10 Tập 1: Trong mặt phẳng tọa độ Oxy, cho A(1;2), B(3;4), C(-1;-2) và D(6;5)

a) Tìm tọa độ của các vecto $\overrightarrow{AB}$ và $\overrightarrow{CD}$.

b) Hãy giải thích tại sao các vecto $\overrightarrow{AB}$ và $\overrightarrow{CD}$ cùng phương.

c) Giả sử E là điểm có tọa độ (a;1). Tìm a để vecto $\overrightarrow{AC}$ và $\overrightarrow{BE}$ cùng phương.

d) Với a tìm được, hãy biểu thị vecto $\overrightarrow{AE}$ theo các vecto $\overrightarrow{AB}$ và $\overrightarrow{AC}$.

Lời giải:

a) Ta có: $\overrightarrow{AB}\left(2;2\right)$ và $\overrightarrow{CD}\left(7;7\right)$.

b) Hai vecto $\overrightarrow{AB}$ và $\overrightarrow{CD}$ cùng phương vì $\frac{7}{2}=\frac{7}{2}$.

c) Ta có: $\overrightarrow{AC}\left(-2;-4\right)$ và $\overrightarrow{BE}\left(a-3;-3\right)$

Để hai vecto $\overrightarrow{AC}$ và $\overrightarrow{BE}$ cùng phương khi

$$\begin{gathered} \frac{-2}{a-3}=\frac{-4}{-3}\iff -4\left(a-3\right)=6 \\ \iff a-3=-\frac{3}{2}\iff a=\frac{3}{2}. \end{gathered}$$

Vậy $a=\frac{3}{2}$ thì hai vecto $\overrightarrow{AC}$ và $\overrightarrow{BE}$ cùng phương

d) Với $a=\frac{3}{2}\Rightarrow E\left(\frac{3}{2};1\right)\Rightarrow \overrightarrow{AE}\left(\frac{1}{2};-1\right)$,

Ta có: $\overrightarrow{AB}\left(2;2\right)$ và $\overrightarrow{AC}\left(-2;-4\right)$

Tồn tại hai số thực u, v thỏa mãn:

$\overrightarrow{AE}=u\overrightarrow{AB}+v\overrightarrow{AC}$

$\iff \left\{\begin{array}{l}\frac{1}{2}=u.2+v.\left(-2\right)\\ 1=u.2+v.\left(-4\right)\end{array}\right.$

$\iff \left\{\begin{array}{l}2u-2v=\frac{1}{2}\\ 2u-4v=1\end{array}\right.\iff \left\{\begin{array}{l}u=0\\ v=-\frac{1}{4}\end{array}\right.$

$\Rightarrow \overrightarrow{AE}=0.\overrightarrow{AB}-\frac{1}{4}\overrightarrow{AC}$

Vậy $\overrightarrow{AE}=-\frac{1}{4}\overrightarrow{AC}$.

Bài 4.37 trang 72 Toán 10 Tập 1: Cho vecto $\overrightarrow{a}\ne \overrightarrow{0}.$ Chứng minh rằng $\frac{1}{\left|\overrightarrow{a}\right|}.\overrightarrow{a}$ (hay còn được viết là $\frac{\overrightarrow{a}}{\left|\overrightarrow{a}\right|}$) là một vecto đơn vị cùng hướng với $\overrightarrow{a}$.

Lời giải:

Nhắc lại kiến thức: $k.\overrightarrow{a}$ cùng hướng với $\overrightarrow{a}$ nếu k > 0.

Ta có: $k=\frac{1}{\left|\overrightarrow{a}\right|}>0\left(\overrightarrow{a}\ne \overrightarrow{0}\right)$

Do đó $\frac{1}{\left|\overrightarrow{a}\right|}.\overrightarrow{a}$ cùng hướng với $\overrightarrow{a}$ hay $\frac{\overrightarrow{a}}{\left|\overrightarrow{a}\right|}$ cùng hướng với $\overrightarrow{a}.$

Bài 4.38 trang 72 Toán 10 Tập 1: Cho ba vecto $\overrightarrow{a},\overrightarrow{b},\overrightarrow{u}$ với $\left|\overrightarrow{a}\right|=\left|\overrightarrow{b}\right|=1$ và $\overrightarrow{a}\perp \overrightarrow{b}$. Xét một hệ trục Oxy với hệ vecto đơn vị $\overrightarrow{i}=\overrightarrow{a},\overrightarrow{j}=\overrightarrow{b}$. Chứng minh rằng:

a) Vecto $\overrightarrow{u}$ có tọa độ là $\left(\overrightarrow{u}.\overrightarrow{a},\overrightarrow{u}.\overrightarrow{b}\right).$  

b) $\overrightarrow{u}=\left(\overrightarrow{u}.\overrightarrow{a}\right).\overrightarrow{a}+\left(\overrightarrow{u}.\overrightarrow{b}\right).\overrightarrow{b}.$

Lời giải:

a) Vì $\overrightarrow{i}=\overrightarrow{a}\Rightarrow \overrightarrow{a}\left(1;0\right)$ và $\overrightarrow{j}=\overrightarrow{b}\Rightarrow \overrightarrow{b}\left(0;1\right)$

Gọi tọa độ của vecto $\overrightarrow{u}\left(c;d\right)$

Khi đó, ta có:

$\overrightarrow{u}.\overrightarrow{a}=1.c+0.d=c;$

$\overrightarrow{u}.\overrightarrow{b}=0.c+1.d=d;$

Vì vậy tọa độ của vecto $\overrightarrow{u}$ là $\left(\overrightarrow{u}.\overrightarrow{a},\overrightarrow{u}.\overrightarrow{b}\right).$

b) Ta có:

$$\begin{gathered} \left(\overrightarrow{u}.\overrightarrow{a}\right).\overrightarrow{a}+\left(\overrightarrow{u}.\overrightarrow{b}\right).\overrightarrow{b}=c.\overrightarrow{a}+d.\overrightarrow{b} \\ =c\left(1;0\right)+d.\left(0;1\right)=\left(c;d\right)=\overrightarrow{u}. \end{gathered}$$

Bài 4.39 trang 72 Toán 10 Tập 1: Trên sông, một ca nô chuyển động thẳng đều theo hướng S15⁰E với vận tốc có độ lớn bằng 20km/h. Tính vận tốc riêng của ca nô, biết rằng, nước trên sông chảy về hướng đông với vận tốc có độ lớn bằng 3km/h.

Lời giải:

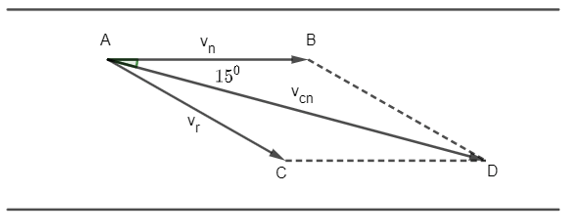
Ta có hình vẽ sau:

Trong đó:

$\overrightarrow{AB}$ là hướng đông

$\overrightarrow{AD}$ là hướng S15⁰E

$\overrightarrow{v_n}$ là vận tốc dòng nước

$\overrightarrow{v_{cn}}$ là vận tốc ca nô

$\overrightarrow{v_r}$ là vận tốc riêng của ca nô

Xét tam giác ABD, có:

$B{D}^2=A{B}^2+A{D}^2-2.AB.AD.cos\widehat{BAD}$ (định lí cosin)

$\iff {\overrightarrow{v_r}}^2={\overrightarrow{v_n}}^2+{\overrightarrow{v_{cn}}}^2-2.\left|\overrightarrow{v_n}\right|.\left|\overrightarrow{v_{cn}}\right|.cos{15}^0$

= 3² + 20² – 2.3.20.cos15⁰

≈ 291,09

⇒ v_r ≈ 17,12

Vậy vận tốc riêng của ca nô là 17,12 km/h.

Lời giải bài tập Toán lớp 10 Bài tập cuối chương IV Kết nối tri thức hay khác:

• Giải Toán 10 trang 71