Bài 5 trang 116 Toán 11 Tập 2 Cánh diều

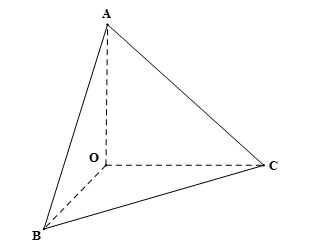
Cho tứ diện OABC thỏa mãn OA = a, OB = b, OC = c, Thể tích của khối tứ diện OABC bằng:

Giải Toán 11 Bài tập cuối chương 8 - Cánh diều

Bài 5 trang 116 Toán 11 Tập 2: Cho tứ diện OABC thỏa mãn OA = a, OB = b, OC = c, $\widehat{AOB}=\widehat{BOC}=\widehat{COA}=90°.$ Thể tích của khối tứ diện OABC bằng:

A. abc;

B. $\frac{abc}{2};$

C. $\frac{abc}{3};$

D. $\frac{abc}{6}.$

Lời giải:

Đáp án đúng là: D

Ta có: $\widehat{AOB}=90°$ nên OA ⊥ OB;

          $\widehat{COA}=90°$ nên OA ⊥ OC.

Mà OB ∩ OC = O trong (OBC).

Suy ra OA ⊥ (OBC).

Vì $\widehat{BOC}=90°$ nên tam giác OBC vuông tại O.

Nên ta có diện tích tam giác OBC vuông tại O là: $S_{\Delta OBC}=\frac{1}{2}OB.OC=\frac{1}{2}bc.$

Thể tích của khối tứ diện OABC với chiều cao OA = a và diện tích đáy $S_{\Delta OBC}=\frac{1}{2}bc$ là: $V_{OABC}=\frac{1}{3}{S}_{\Delta OBC}.OA=\frac{1}{3}.\frac{1}{2}bc.a=\frac{abc}{6}.$

Lời giải bài tập Toán 11 Bài tập cuối chương 8 hay, chi tiết khác:

• Bài 1 trang 116 Toán 11 Tập 2: Cho hình lập phương MNPQ.M’N’P’Q’ có cạnh bằng a.....

• Bài 2 trang 116 Toán 11 Tập 2: Cho hình hộp chữ nhật MNPQ.M’N’P’Q’ có MN = 2a, MQ = 3a, MM’ = 4a. Khoảng cách giữa hai đường thẳng NP và M’N’ bằng:....

• Bài 3 trang 116 Toán 11 Tập 2: Cho khối lăng trụ có diện tích đáy bằng a2 và chiều cao bằng 3a. Thể tích của khối lăng trụ đó bằng:....

• Bài 4 trang 116 Toán 11 Tập 2: Cho khối chóp có diện tích đáy là a² và chiều cao là 3a. Thể tích của khối chóp bằng:....

• Bài 6 trang 116 Toán 11 Tập 2: Cho hình chóp S.ABC có SA ⊥ (ABC), AC ⊥ BC, $SA=BC=a\sqrt{3},$ AC = a (Hình 99)....

• Bài 7 trang 117 Toán 11 Tập 2: Cho hình lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh bằng a. Gọi M là trung điểm của AB (Hình 100)....

• Bài 8 trang 117 Toán 11 Tập 2: Đền Kukulcan (Hình 101) là một kim tự tháp Trung Mỹ nằm ở khu di tích Chichen Itza, Mexico, được người Maya xây vào khoảng từ thế kỉ IX đến thế kỉ XII....