Hoạt động 4 trang 103 Toán 11 Tập 2 Cánh diều
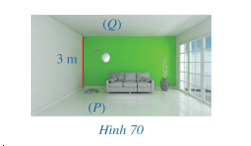
a) Trong Hình 70, sàn nhà và trần nhà của căn phòng gợi nên hình ảnh hai mặt phẳng song song (P), (Q). Chiều cao của căn phòng là 3 m.
Giải Toán 11 Bài 5: Khoảng cách - Cánh diều
Hoạt động 4 trang 103 Toán 11 Tập 2: a) Trong Hình 70, sàn nhà và trần nhà của căn phòng gợi nên hình ảnh hai mặt phẳng song song (P), (Q). Chiều cao của căn phòng là 3 m.
Chiều cao đó gợi nên khái niệm gì trong hình học liên quan đến hai mặt phẳng song song (P), (Q)?
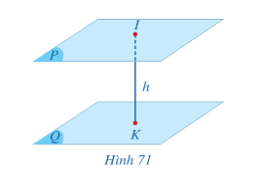
b) Cho hai mặt phẳng (P) và (Q) song song với nhau. Xét điểm I tuỳ ý trong mặt phẳng (P), lấy K là hình chiếu của I trên (Q) (Hình 71). Khoảng cách IK từ điểm I đến mặt phẳng (Q) có phụ thuộc vào vị trí của điểm I trong mặt phẳng (P) hay không? Vì sao?
Lời giải:
a) Vì sàn nhà và trần nhà của căn phòng gợi nên hình ảnh hai mặt phẳng song song (P), (Q) và ta biết chiều cao của căn phòng là 3 m.
Vậy nên chiều cao của căn phòng đó gợi nên khái niệm khoảng cách giữa hai mặt phẳng song song trong hình học.
b)
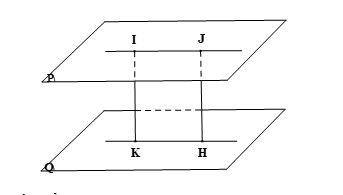
Trên mặt phẳng (P) lấy điểm J khác I.
Gọi H là hình chiếu của J trên (Q) nên JH ⊥ (Q).
Suy ra d(J, (Q)) = JH.
Do K là hình chiếu của I trên (Q) nên IK ⊥ (Q).
Suy ra d(I, (Q)) = IK.
Ta có: JH ⊥ (Q) và IK ⊥ (Q) nên JH //IK. (1)
Khi đó, hai đường thẳng JH và IK sẽ xác định một mặt phẳng là mặt phẳng (ABKH).
Ta thấy:
· I và J là hai điểm chung của hai mặt phẳng (IJHK) và (P).
Suy ra IJ = (IJHK) ∩ (P).
· H và K là hai điểm chung của hai mặt phẳng (IJHK) và (Q).
Suy ra HK = (IJHK) ∩ (Q).
Ta có: (P) // (Q);
IJ = (IJHK) ∩ (P);
HK = (IJHK) ∩ (Q).
Suy ra IJ // HK. (2)
Từ (1), (2) ta có IJHK là hình bình hành.
Suy ra IK = JH hay d(I, (Q)) = d(J, (Q)).
Vậy khoảng cách IK từ điểm I đến mặt phẳng (Q) không phụ thuộc vào vị trí của điểm I trong mặt phẳng (P).
Lời giải bài tập Toán 11 Bài 5: Khoảng cách hay, chi tiết khác: