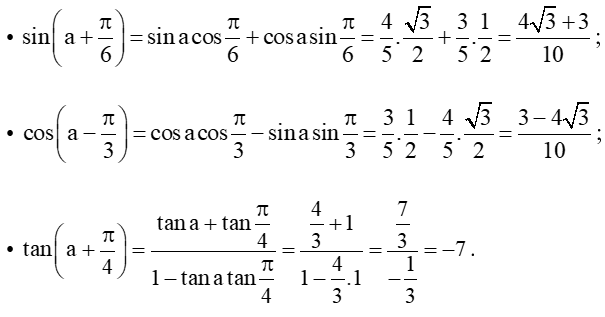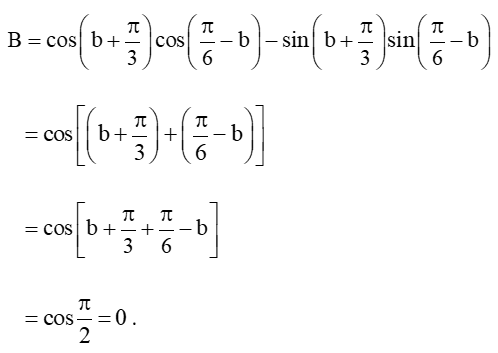Giải Toán 11 trang 20 Tập 1 Cánh diều

---

Với Giải Toán 11 trang 20 Tập 1 trong Bài 2: Các phép biến đổi lượng giác Toán lớp 11 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 20.

Giải Toán 11 trang 20 Tập 1 Cánh diều

Bài 1 trang 20 Toán 11 Tập 1: Cho cosa = $\frac{3}{5}$ với 0<a<$\frac{\pi }{2}$. Tính sin$\left(a+\frac{\pi }{6}\right)$, cos$\left(a-\frac{\pi }{3}\right)$, tan$\left(a+\frac{\pi }{4}\right)$.

Lời giải:

Do 0<a<$\frac{\pi }{2}$ nên sina>0.

Áp dụng công thức sin²a + cos²a = 1, ta có:

$si{n}^{2}a+{\left(\frac{3}{5}\right)}^2=1$

$\Rightarrow si{n}^{2}a=1-{\left(\frac{3}{5}\right)}^2=1-\frac{9}{25}=\frac{16}{25}$

$\Rightarrow$sina = $\frac{4}{5}$ (do sina > 0).

Khi đó tana = $\frac{\sin a}{\cos a}=\frac{\frac{4}{5}}{\frac{3}{5}}=\frac{4}{3}$.

Áp dụng công thức cộng, ta có:

Bài 2 trang 20 Toán 11 Tập 1: Tính:

A = sin(a – 17°)cos(a + 13°) – sin(a + 13°)cos(a – 17°);

B = cos$\left(b+\frac{\pi }{3}\right)$cos$\left(\frac{\pi }{6}-b\right)$ - sin$\left(b+\frac{\pi }{3}\right)$sin$\left(\frac{\pi }{6}-b\right)$.

Lời giải:

Ta có:

A = sin(a – 17°)cos(a + 13°) – sin(a + 13°)cos(a – 17°)

= sin(a – 17°)cos(a + 13°) – cos(a – 17°)sin(a + 13°)

= sin[(a – 17°) – (a + 13°)]

= sin(a – 17° – a – 13°)

= sin(‒30°)

= ‒ sin30°

=-$\frac{1}{2}$ .

Bài 3 trang 20 Toán 11 Tập 1: Cho tan(a + b) = 3, tan(a – b) = 2. Tính: tan2a, tan2b.

Lời giải:

Ta có:

tan2a = tan[(a + b) + (a – b)]

$=\frac{\tan \left(a+b\right)+\tan \left(a-b\right)}{1-\tan \left(a+b\right)\tan \left(a-b\right)}=\frac{3+2}{1-3.2}=\frac{5}{-5}=-1$;

tan2b = tan[(a + b) ‒ (a – b)]

$=\frac{\tan \left(a+b\right)-\tan \left(a-b\right)}{1+\tan \left(a+b\right)\tan \left(a-b\right)}=\frac{3-2}{1+3.2}=\frac{1}{7}$.

Bài 4 trang 20 Toán 11 Tập 1: Cho sina = $\frac{2}{\sqrt{5}}$. Tính cos2a, cos4a.

Lời giải:

Áp dụng công thức hạ bậc, ta có:

cos2a = 1 – 2sin²a = 1 -2.${\left(\frac{2}{\sqrt{5}}\right)}^2=1-2.\frac{4}{5}=-\frac{3}{5}$.

cos4a = 2cos²a – 1 = ${\left(-\frac{3}{5}\right)}^2-1=\frac{9}{25}-1=-\frac{16}{25}$.

Bài 5 trang 20 Toán 11 Tập 1: Cho sina + cosa = 1. Tính: sin2a.

Lời giải:

Ta có: sina + cosa = 1

$\Rightarrow$ (sina + cosa)² = 1²

$\Rightarrow$ sin²a + 2sina cosa + cos²a = 1

$\Rightarrow$ 2sina cosa + (sin²a + cos²a) = 1

$\Rightarrow$ sin2a + 1 = 1

$\Rightarrow$ sin2a = 0.

Vậy với sina + cosa = 1 thì sin2a = 0.

Lời giải bài tập Toán 11 Bài 2: Các phép biến đổi lượng giác Cánh diều hay khác:

• Giải Toán 11 trang 16

• Giải Toán 11 trang 17

• Giải Toán 11 trang 18

• Giải Toán 11 trang 19

• Giải Toán 11 trang 21