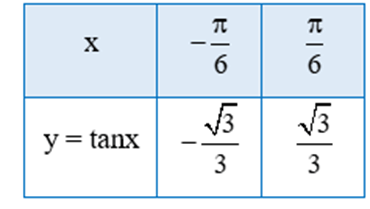Giải Toán 11 trang 28 Tập 1 Cánh diều

---

Với Giải Toán 11 trang 28 Tập 1 trong Bài 3: Hàm số lượng giác và đồ thị Toán lớp 11 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 28.

Giải Toán 11 trang 28 Tập 1 Cánh diều

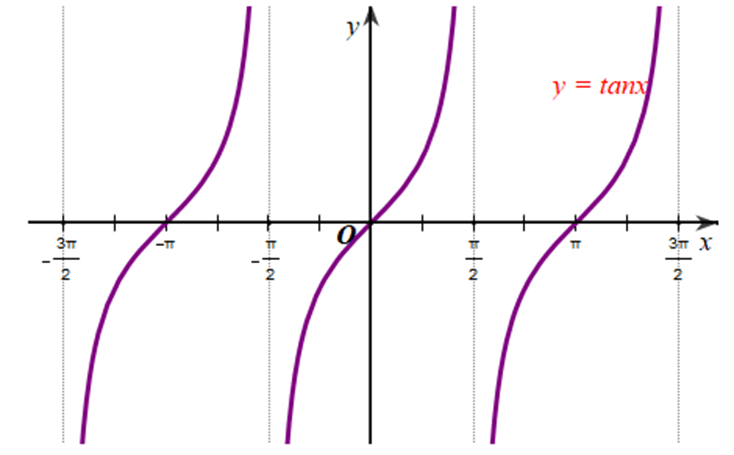
Hoạt động 10 trang 28 Toán 11 Tập 1: Cho hàm số y = tanx.

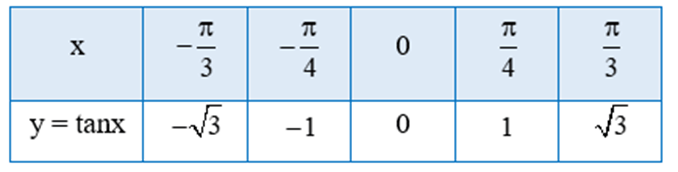
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:

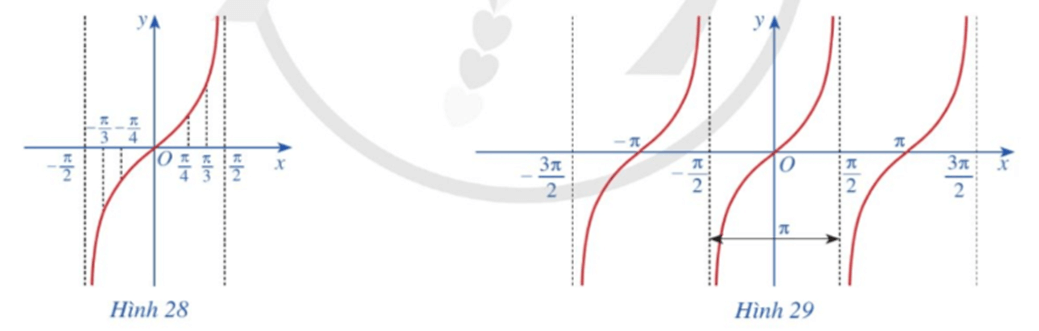
b) Trong mặt phẳng toạ độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x; tanx) với $x\in \left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ và nối lại ta được đồ thị hàm số y = tan x trên khoảng $x\in \left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ (Hình 28).

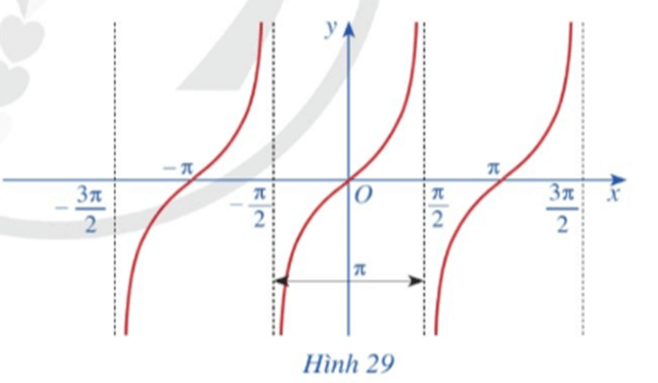
c) Làm tương tự như trên đối với các khoảng $\left(\frac{\pi }{2};\frac{3\pi }{2}\right),\left(-\frac{3\pi }{2};-\frac{\pi }{2}\right)$, …, ta có đồ thị hàm số y = tan x trên D được biểu diễn ở Hình 29.

Lời giải:

a) Thay từng giá trị của x vào hàm số y = tanx ta có bảng sau:

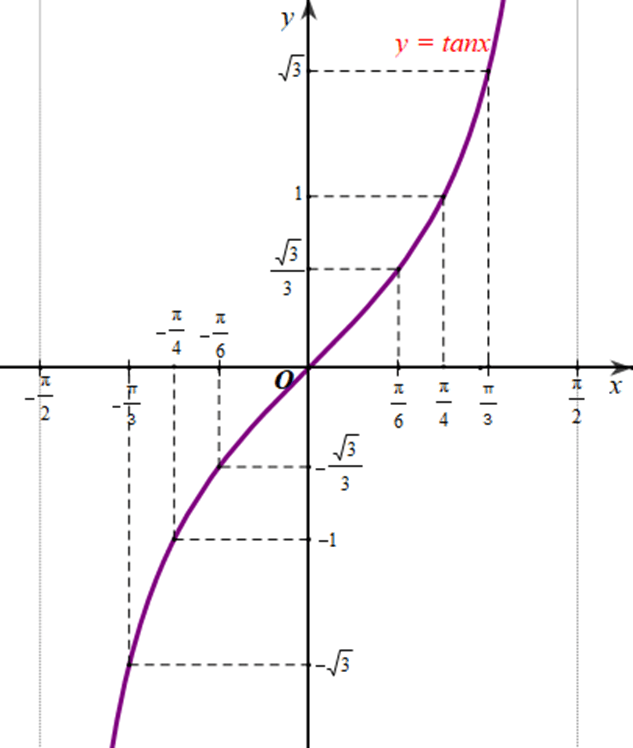
b) Lấy thêm một số điểm (x; tanx) với $x\in \left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ trong bảng sau và nối lại ta được đồ thị hàm số y = tanx trên khoảng $x\in \left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ (hình vẽ).

c) Làm tương tự như trên đối với các $\left(\frac{\pi }{2};\frac{3\pi }{2}\right),\left(-\frac{3\pi }{2};-\frac{\pi }{2}\right)$, …, ta có đồ thị hàm số y = tanx trên D được biểu diễn ở hình vẽ sau:

Hoạt động 11 trang 28 Toán 11 Tập 1: Quan sát đồ thị hàm số y = tanx ở Hình 29.

a) Nêu tập giá trị của hàm số y = tanx.

b) Gốc toạ độ có là tâm đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số y = tanx.

c) Bằng cách dịch chuyển đồ thị hàm số y = tanx trên khoảng $\left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ song song với trục hoành sang phải theo đoạn có độ dài π, ta nhận được đồ thị hàm số y = tanx trên khoảng $\left(\frac{\pi }{2};\frac{3\pi }{2}\right)$ hay không? Hàm số y = tanx có tuần hoàn hay không?

d) Tìm khoảng đồng biến, nghịch biến của hàm số y = tanx.

Lời giải:

a) Tập giá trị của hàm số y = tanx là ℝ.

b) Gốc toạ độ là tâm đối xứng của đồ thị hàm số y = tanx.

Do đó hàm số y = tanx là hàm số lẻ.

c)

‒ Bằng cách dịch chuyển đồ thị hàm số y = tanx trên khoảng $\left(-\frac{\pi }{2};\frac{\pi }{2}\right)$ song song với trục hoành sang phải theo đoạn có độ dài π, ta sẽ nhận được đồ thị hàm số y = tanx trên khoảng $\left(\frac{\pi }{2};\frac{3\pi }{2}\right)$.

Làm tương tự như trên ta sẽ được đồ thị hàm số y = tanx trên R\$\left(\frac{\pi }{2}+k\pi |k\in \mathbb{Z}\right)$.

‒ Xét hàm số f(x) = y = tanx trên D = R\$\left(\frac{\pi }{2}+k\pi |k\in \mathbb{Z}\right)$, với T = π và x ∈ D ta có:

• x + π ∈ D và x – π ∈ D;

• f(x + π) = f(x)

Do đó hàm số y = tanx là hàm số tuần hoàn với chu kì T = π.

d) Quan sát đồ thị hàm số y = tanx ở Hình 29, ta thấy: đồ thị hàm số đồng biến trên mỗi khoảng $\left(-\frac{3\pi }{2};-\frac{\pi }{2}\right);\left(-\frac{\pi }{2};\frac{\pi }{2}\right);\left(\frac{\pi }{2};\frac{3\pi }{2}\right)$;...

Ta có: $\left(-\frac{3\pi }{2};-\frac{\pi }{2}\right)=\left(-\frac{\pi }{2}-\pi ;\frac{\pi }{2}-\pi \right)$;

$\left(\frac{\pi }{2};\frac{3\pi }{2}\right)=\left(-\frac{\pi }{2}+\pi ;\frac{\pi }{2}+\pi \right)$;

…

Do đó ta có thể viết đồ thị hàm số y = tanx đồng biến trên mỗi khoảng $\left(-\frac{\pi }{2}+k\pi ;\frac{\pi }{2}+k\pi \right)$ với k ∈ ℤ.

Lời giải bài tập Toán 11 Bài 3: Hàm số lượng giác và đồ thị Cánh diều hay khác:

• Giải Toán 11 trang 22

• Giải Toán 11 trang 23

• Giải Toán 11 trang 24

• Giải Toán 11 trang 25

• Giải Toán 11 trang 26

• Giải Toán 11 trang 27

• Giải Toán 11 trang 29

• Giải Toán 11 trang 30

• Giải Toán 11 trang 31