Giải Toán 11 trang 75 Tập 1 Cánh diều

---

Với Giải Toán 11 trang 75 Tập 1 trong Bài 3: Hàm số liên tục Toán lớp 11 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 75.

Giải Toán 11 trang 75 Tập 1 Cánh diều

Luyện tập 2 trang 75 Toán 11 Tập 1: Hàm số f(x) = 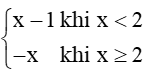. Có liên tục trên ℝ hay không?

Lời giải:

+) Với mỗi x₀ ∈ (– ∞; 2) có $\underset{x\to x_0}{\lim }f\left(x\right)=\underset{x\to x_0}{\lim }\left(x-1\right)=x_0-1=f\left(x_0\right)$là hàm số liên tục.

+) Với mỗi x₀ ∈ (2; +∞) có $\underset{x\to x_0}{\lim }f\left(x\right)=\underset{x\to x_0}{\lim }\left(-x\right)=-x_0=f\left(x_0\right)$là hàm số liên tục.

+) Tại x = 2, ta có: $\underset{x\to 2}{\lim }f\left(x\right)=\underset{x\to 2}{\lim }$(x-1) = 1và f(2) = – 2 nên $\underset{x\to 2}{\lim }f\left(x\right)\ne f\left(2\right)$.

Vậy hàm số không liên tục tại x = 2.

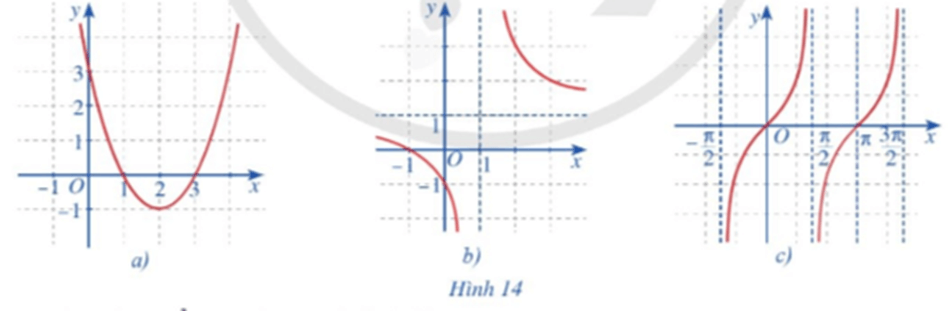
Hoạt động 3 trang 75 Toán 11 Tập 1: Quan sát đồ thị các hàm số: y = x² – 4x + 3 (Hình 14a); y = $\frac{x+1}{x-1}\left(x\ne 1\right)$(Hình 14b); y = tanx (Hình 14c) và nêu nhận xét về tính liên tục của mỗi hàm số đó trên từng khoảng của tập xác định.

Lời giải:

Hình 14a) đồ thị là đường cong Parabol liền mạch nên hàm số liên tục trên toàn bộ khoảng xác định.

Hình 14b) đồ thị bị chia làm hai nhánh:

- Với x < 1 ta thấy hàm số là một đường cong liền nên liên tục.

- Với x > 1 ta thấy hàm số là một đường cong liền nên liên tục.

Vậy hàm đố liên tục trên từng khoảng xác định.

Hình 14c) đồ thị hàm số y = tanx chia thành nhiều nhánh, và mỗi nhánh là các đường cong liền. Do đó hàm số liên tục trên mỗi khoảng xác định của chúng.

Lời giải bài tập Toán 11 Bài 3: Hàm số liên tục Cánh diều hay khác:

• Giải Toán 11 trang 73

• Giải Toán 11 trang 74

• Giải Toán 11 trang 76

• Giải Toán 11 trang 77