Bài 1 trang 119 Toán 11 Tập 1 Chân trời sáng tạo

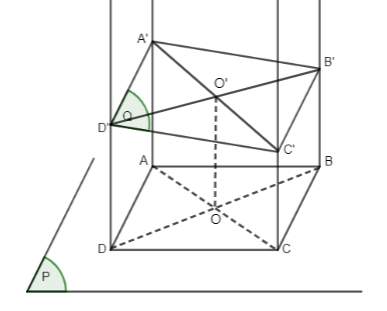
Trong mặt phẳng (P) cho hình bình hành ABCD. Ta dựng các nửa đường thẳng song song với nhau và nằm về một phía đối với (P) lần lượT đi qua các điểm A, B, C, D. Một mặt phẳng (Q) cắt bốn nửa đường thẳng nói trên tại A’, B’, C’, D’. Chứng minh rằng:

Giải Toán 11 Bài 4: Hai mặt phẳng song song - Chân trời sáng tạo

Bài 1 trang 119 Toán 11 Tập 1: Trong mặt phẳng (P) cho hình bình hành ABCD. Ta dựng các nửa đường thẳng song song với nhau và nằm về một phía đối với (P) lần lượT đi qua các điểm A, B, C, D. Một mặt phẳng (Q) cắt bốn nửa đường thẳng nói trên tại A’, B’, C’, D’. Chứng minh rằng:

AA’ + CC’ = BB’ + DD’.

Lời giải:

+) Ta có:

(AA’B’B) // (DD’C’C)

(Q) ∩ (AA’B’B) = A’B’

(Q) ∩ (DD’C’C) = D’C’

⇒ A’B’ // D’C’ (1).

+) Tương tự ta có:

(AA’D’D) // (BB’C’C)

(Q) ∩ (AA’D’D) = A’D’

(Q) ∩ (BB’C’C) = B’C’

⇒ A’D’ // B’C’ (2).

Từ (1) và (2) suy ra tứ giác A’B’C’D’ là hình bình hành.

Gọi O và O’ lần lượt là tâm của các hình bình hành ABCD và A’B’C’D’ nên O là trung điểm của AC và BD và O’ là trung điểm của A’C’ và B’D’.

+) Xét tứ giác ACC’A’, có: CC’ // AA’ nên ACC’A’ là hình thang, O là trung điểm của AC và O’ là trung điểm của A’C’ nên OO’ là đường trung bình của hình thang suy ra: $OO\text{'}=\frac{1}{2}\left(AA\text{'}+CC\text{'}\right)$ (1).

+) Xét tứ giác BB’D’D, có: BB’ // DD’ nên BB’D’D là hình thang, O là trung điểm của BD và O’ là trung điểm của B’D’ nên OO’ là đường trung bình của hình thang suy ra: $OO\text{'}=\frac{1}{2}\left(BB\text{'}+DD\text{'}\right)$ (2).

Từ (1) và (2) suy ra AA’ + CC’ = BB’ + DD’.

Lời giải bài tập Toán 11 Bài 4: Hai mặt phẳng song song hay, chi tiết khác:

• Hoạt động khởi động trang 113 Toán 11 Tập 1: Bề mặt trên của mỗi bậc thang này được đặt như thế nào so với mặt đất? ....

• Hoạt động khám phá 1 trang 113 Toán 11 Tập 1: Hộp giấy có các mặt là hình vuông ở Hình 1a được vé lại với các đỉnh là A, B, C, D, A’, B’, C’, D’ như Hình 1b ....

• Vận dụng 1 trang 114 Toán 11 Tập 1: Tìm một số mặt phẳng song song có trong hình chụp căn phòng ở Hình 4 ....

• Hoạt động khám phá 2 trang 114 Toán 11 Tập 1: Cho mặt phẳng (P) chứa hai đường thẳng a, b cắt nhau và cùng song song với mặt phẳng (Q) ....

• Thực hành 1 trang 115 Toán 11 Tập 1: Cho tứ diện ABCD có E, F, H lần lượt là trung điểm của AB, AC, AD ....

• Hoạt động khám phá 3 trang 115 Toán 11 Tập 1: Cho điểm A ở ngoài mặt phẳng (Q). Trong (Q) vẽ hai đường thẳng cắt nhau a’ và b’ ....

• Hoạt động khám phá 4 trang 115 Toán 11 Tập 1: Cho ba mặt phẳng (P), (Q), (R) thỏa mãn (P) // (Q), (R) ∩ (P) = a và (R) ∩ (Q) = b ....

• Thực hành 2 trang 116 Toán 11 Tập 1: Cho hình chóp S.ABCD với đáy ABCD là hình bình hành có O là giao điểm của hai đường chéo ....

• Vận dụng 2 trang 116 Toán 11 Tập 1: Khi dùng dao cắt các lớp bánh (Hình 11), giả sử bề mặt các lớp bánh là các mặt phẳng song song ....

• Hoạt động khám phá 5 trang 116 Toán 11 Tập 1: Cho ba mặt phẳng song song (P), (Q), (R) lần lượt cắt hai đường thẳng a và a’ tại các điểm A, B, C ....

• Thực hành 3 trang 117 Toán 11 Tập 1: Cho hình chóp S.ABC có SA = 9, SB = 12, SC = 15. Trên cạnh SA lấy điểm M, N sao cho SM = 4 ....

• Hoạt động khám phá 6 trang 117 Toán 11 Tập 1: Hình dạng của các đồ vật như hộp phấn, lồng đèn, hộp quà, lăng kính có đặc điểm gì giống nhau? ....

• Hoạt động khám phá 7 trang 118 Toán 11 Tập 1: Cho hình lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình bình hành ....

• Thực hành 4 trang 119 Toán 11 Tập 1: Cho hình hộp ABCD.A’B’C’D’và một mặt phẳng (α) cắt các mặt của hình hộp theo các giao tuyến ....

• Vận dụng 3 trang 119 Toán 11 Tập 1: Tìm hình lăng trụ có thể lấy một mặt bất kì làm mặt đáy ....

• Bài 2 trang 120 Toán 11 Tập 1: Cho hình chóp S.ABCD, đáy ABCD là hình bình hành có O là giao điểm của hai đường chéo ....

• Bài 3 trang 120 Toán 11 Tập 1: Cho hai hình vuông ABCD và ABEF ở trong hai mặt phẳng khác nhau ....

• Bài 4 trang 120 Toán 11 Tập 1: Cho hình hộp ABCD.A’B’C’D’. Gọi G1 và G2 lần lượt là trọng tâm của hai tam giác BDA’ và B’D’C ....

• Bài 5 trang 120 Toán 11 Tập 1: Để làm một khung lồng đèn kéo quân hình lăng trụ lục giác ABCDEF.A’B’C’D’E’F’ ....

• Bài 6 trang 120 Toán 11 Tập 1: Chỉ ra các mặt phẳng song song trong mỗi hình sau. Tìm thêm một số ví dụ khác về mặt phẳng song song trong thực tế ....