Bài 8 trang 24 Toán 11 Tập 1 Chân trời sáng tạo

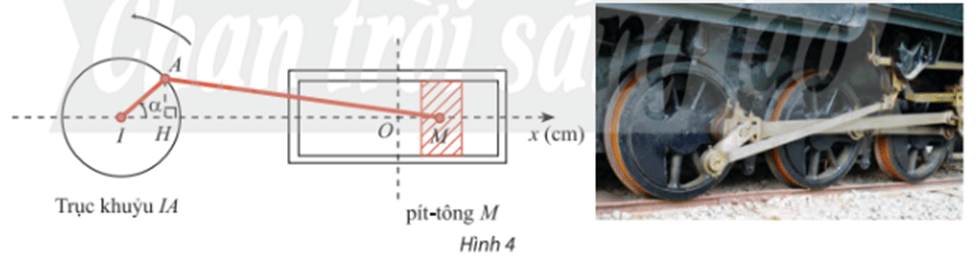
Trong Hình 4, pít – tông M của động cơ chuyển động tịnh tiến qua lại dọc theo xi lanh làm quay trục khuỷu IA. Ban đầu I, A, M thẳng hàng. Cho α là góc quay của trục khuỷu, O là vị trí của pít – tông khi và H là hình chiếu của A lên Ix. Trục khuỷu IA rất ngắn so với độ dài thanh truyền AM nên có thể xem như độ dài MH không đổi và gần bằng MA.

Giải Toán 11 Bài 3: Các công thức lượng giác - Chân trời sáng tạo

Bài 8 trang 24 Toán 11 Tập 1: Trong Hình 4, pít – tông M của động cơ chuyển động tịnh tiến qua lại dọc theo xi lanh làm quay trục khuỷu IA. Ban đầu I, A, M thẳng hàng. Cho α là góc quay của trục khuỷu, O là vị trí của pít – tông khi $\alpha =\frac{\pi }{2}$ và H là hình chiếu của A lên Ix. Trục khuỷu IA rất ngắn so với độ dài thanh truyền AM nên có thể xem như độ dài MH không đổi và gần bằng MA.

a) Biết IA = 8cm, viết công thức tính tọa độ x_M của điểm M trên trục Ox theo α.

b) Ban đầu α = 0. Sau 1 phút chuyển động, x_M = – 3cm. Xác định x_M sau 2 phút chuyển động. Làm tròn kết quả đến hàng phần mười.

Lời giải:

Tại $\alpha =\frac{\pi }{2}$ thì H trùng I, M trùng O nên MH = OI do đó OM = IH.

Xét tam giác AHI vuông tại H có: IH = cosα.IA = 8cosα.

Lời giải bài tập Toán 11 Bài 3: Các công thức lượng giác hay, chi tiết khác:

• Hoạt động khởi động trang 20 Toán 11 Tập 1: Trong kiến trúc, các vòm cổng bằng đá thường có hình nửa đường tròn ....

• Hoạt động khám phá 1 trang 21 Toán 11 Tập 1: Quan sát Hình 1. Từ hai cách tính tích vô hướng của vectơ $\overrightarrow{OM}$ và $\overrightarrow{ON}$ sau đây ....

• Thực hành 1 trang 21 Toán 11 Tập 1: Tính sin$\frac{\pi }{12}$ và tan$\frac{\pi }{12}$ ....

• Hoạt động khám phá 2 trang 21 Toán 11 Tập 1: Hãy áp dụng công thức cộng cho trường hợp β = α ....

• Thực hành 2 trang 22 Toán 11 Tập 1: Tính cos$\frac{\pi }{8}$ và tan$\frac{\pi }{8}$ ....

• Hoạt động khám phá 3 trang 22 Toán 11 Tập 1: Từ công thức cộng, hãy tính tổng và hiệu của ....

• Thực hành 3 trang 22 Toán 11 Tập 1: Tính giá trị của các biểu thức sin$\frac{\pi }{24}$cos$\frac{5\pi }{24}$ và sin$\frac{7\pi }{8}$sin$\frac{5\pi }{8}$ ....

• Hoạt động khám phá 4 trang 22 Toán 11 Tập 1: Áp dụng công thức biến đổi tích thành tổng cho hai góc lượng giác ....

• Thực hành 4 trang 23 Toán 11 Tập 1: Tính cos$\frac{7\pi }{12}$ + cos$\frac{\pi }{12}$ ....

• Vận dụng trang 23 Toán 11 Tập 1: Trong bài toán khởi động, cho biết vòm cổng rộng 120 cm ....

• Bài 1 trang 23 Toán 11 Tập 1: Không dùng máy tính cầm tay, tính các giá trị lượng giác của các góc ....

• Bài 2 trang 23 Toán 11 Tập 1: Tính $\sin \left(\alpha +\frac{\pi }{6}\right),\text{cos}\left(\frac{\pi }{4}-\alpha \right)$ biết sin$\alpha =-\frac{5}{13}$ và $\pi <\alpha <\frac{3\pi }{2}$ ....

• Bài 3 trang 24 Toán 11 Tập 1: Tính các giá trị lượng giác của góc 2α, biết ....

• Bài 4 trang 24 Toán 11 Tập 1: Rút gọn các biểu thức sau ....

• Bài 5 trang 24 Toán 11 Tập 1: Tính các giá trị lượng giác của góc α, biết ....

• Bài 6 trang 24 Toán 11 Tập 1: Chứng minh rằng tam giác ABC, ta có sinA = sinB.cosC + sinC.cosB ....

• Bài 7 trang 24 Toán 11 Tập 1: Trong Hình 3, tam giác ABC vuông tại B và có hai cạnh góc vuông là AB = 4 ....

• Bài 9 trang 24 Toán 11 Tập 1: Trong Hình 5, ba điểm M, N, P nằm ở đầu các cánh quạt của tua bin gió ....