Thực hành 1 trang 55 Toán 11 Tập 2 Chân trời sáng tạo
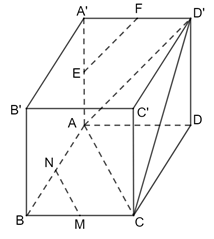
Cho hình hộp ABCD.A′B′C′D′ có 6 mặt đều là hình vuông M, N, E, F lần lượt là trung điểm các cạnh BC, BA, AA′, A′D′. Tính góc giữa các cặp đường thẳng:
Giải Toán 11 Bài 1: Hai đường thẳng vuông góc - Chân trời sáng tạo
Thực hành 1 trang 55 Toán 11 Tập 2: Cho hình hộp ABCD.A′B′C′D′ có 6 mặt đều là hình vuông M, N, E, F lần lượt là trung điểm các cạnh BC, BA, AA′, A′D′. Tính góc giữa các cặp đường thẳng:
a) MN và DD ′ ;
b) MN và CD ′ ;
c) EF và CC ′ .
Lời giải:
a) Xét tam giác ABC có:
M là trung điểm của BC
N là trung điểm của BA
Nên MN là đường trung bình của tam giác ABC.
⇒ MN // AC
Mà DD ′ // AA ′ nên (MN, DD ′ ) = (AC, AA ′ ) =
b) Ta có: MN // AC
⇒ (MN, CD ′ ) = (AC, CD ′ ) =
Vì ABCD, ADD ′A′, CDD′C′ là các hình vuông bằng nhau nên các đường chéo của chúng bằng nhau nên AC = AD′ = CD′.
Suy ra ACD ′ là tam giác đều.
⇒ hay (MN, CD ′ ) = 60 °
c) Xét tam giác AA′D′ có:
E là trung điểm của AA ′
F là trung điểm của A ′D′
Nên EF là đường trung bình của tam giác AA ′D′ .
⇒ EF // AD ′
Mà CC ′ // AA ′
⇒ (EF, CC ′ ) = (AD ′ , AA ′ ) =
Lời giải bài tập Toán 11 Bài 1: Hai đường thẳng vuông góc hay, chi tiết khác: