Thực hành 4 trang 55 Toán 11 Tập 1 Chân trời sáng tạo
Giải Toán 11 Bài 2: Cấp số cộng - Chân trời sáng tạo
Thực hành 4 trang 55 Toán 11 Tập 1:
a) Tính tổng 50 số tự nhiên chẵn đầu tiên.
b) Cho cấp số cộng (un) có u3 + u28 = 100. Tính tổng 30 số hạng đầu tiên của cấp số cộng đó.
c) Cho cấp số cộng (vn) có S6 = 110. Tính S20.
Lời giải:
a) 50 số tự nhiên chẵn lập thành một cấp số cộng, có u1 = 0, công sai d = 2.
Khi đó tổng của 50 số này là:
S50=50(0+50)2=1250.
b) Ta có: u3 + u28 = u1 + 2d + u1 + 27d = 2u1 + 29d = 100
Tổng của 30 số hạng đầu tiên của cấp số cộng đó là:
S30=30(u1+u30)2=30.(u1+u1+29d)2=30(2u1+29d)2=30.1002=1500.
c) Ta có: S6=6(u1+u6)2=6.(u1+u1+5d)2=6(2u1+5d)2=18⇔2u1+5d=6
Tổng của 10 số hạng đầu tiên của cấp số cộng đó là:
S10=10(u1+u10)2=10.(u1+u1+9d)2=10(2u1+9d)2=110⇔2u1+9d=22.
Khi đó ta có hệ phương trình: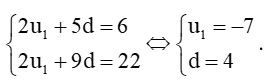 
.
Tổng 20 số hạng đầu tiên của cấp số cộng là:
S10=10(u1+u10)2=10.(u1+u1+9d)2=10(2u1+9d)2=110⇔2u1+9d=22.
Lời giải bài tập Toán 11 Bài 2: Cấp số cộng hay, chi tiết khác: