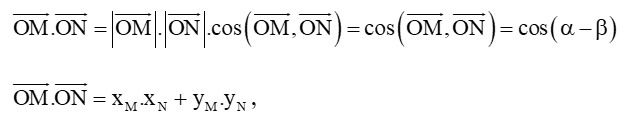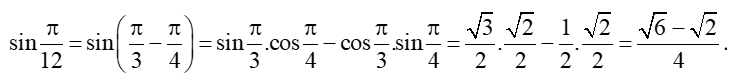Giải Toán 11 trang 21 Tập 1 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với Giải Toán 11 trang 21 Tập 1 trong Bài 3: Các công thức lượng giác Toán lớp 11 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 21.

Giải Toán 11 trang 21 Tập 1 Chân trời sáng tạo

Hoạt động khám phá 1 trang 21 Toán 11 Tập 1: Quan sát Hình 1. Từ hai cách tính tích vô hướng của vectơ $\overrightarrow{OM}$ và $\overrightarrow{ON}$ sau đây:

Hãy suy ra công thức tính cos(α – β) theo các giá trị lượng giác của α và β. Từ đó, hãy suy ra công thức cos(α + β) bằng cách thay β bằng – β.

Lời giải:

Ta có: cos(α – β) = x_M.x_N + y_M.y_N = cosα.cosβ + sinα.sinβ.

Ta có: cos(α + β) = cos(α – (– β)) = cosα.cos(–β) + sinα.sin(–β) = cosα.cosβ – sinα.sinβ.

Thực hành 1 trang 21 Toán 11 Tập 1: Tính sin$\frac{\pi }{12}$ và tan$\frac{\pi }{12}$.

Lời giải:

Ở ví dụ 1 ta có: cos$\frac{\pi }{12}=\frac{\sqrt{6}+\sqrt{2}}{4}$

Suy ra tan.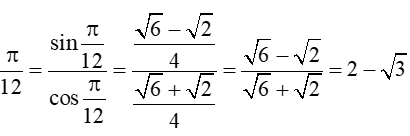

Hoạt động khám phá 2 trang 21 Toán 11 Tập 1: Hãy áp dụng công thức cộng cho trường hợp β = α và tính các giá trị lượng giác của góc 2α.

Lời giải:

Ta có:

cos2α = cos(α + α) = cosα.cosα – sinα.sinα = cos²α – sin²α = cos²α + sin²α – 2sin²α = 1 – 2sin²α = 2cos²α – 1.

sin2α = sin(α + α) = sinα.cosα + cosα.sinα = 2.sinα.cosα .

.

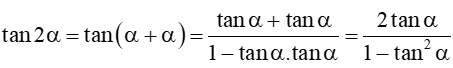
Lời giải bài tập Toán 11 Bài 3: Các công thức lượng giác Chân trời sáng tạo hay khác:

• Giải Toán 11 trang 20

• Giải Toán 11 trang 22

• Giải Toán 11 trang 23

• Giải Toán 11 trang 24