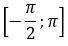Giải Toán 11 trang 30 Tập 1 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với Giải Toán 11 trang 30 Tập 1 trong Bài 4: Hàm số lượng giác và đồ thị Toán lớp 11 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 30.

Giải Toán 11 trang 30 Tập 1 Chân trời sáng tạo

Thực hành 3 trang 30 Toán 11 Tập 1: Cho hàm số y = cos x với x$\in$

a) Vẽ đồ thị hàm số đã cho.

b) Tại các điểm nào thì giá trị của hàm số lớn nhất?

c) Tìm các giá trị của x thuộc 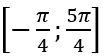sao cho sin$\left(x-\frac{\pi }{4}\right)$<0.

Lời giải:

Nội dung đang được cập nhật...

Vận dụng 1 trang 30 Toán 11 Tập 1: Li độ s(cm) của một con lắc đồng hồ theo thời gian t(giây) được cho bởi hàm số s = 2cos$\pi$t. Dựa vào đồ thị của hàm số côsin, hãy xác định ở các thời điểm t nào trong 3 giây đầu thì con lắc có li độ lớn nhất.

(Theo https://www.britannica.com/science/simple-harmonic-motion)

Lời giải:

Nội dung đang được cập nhật...

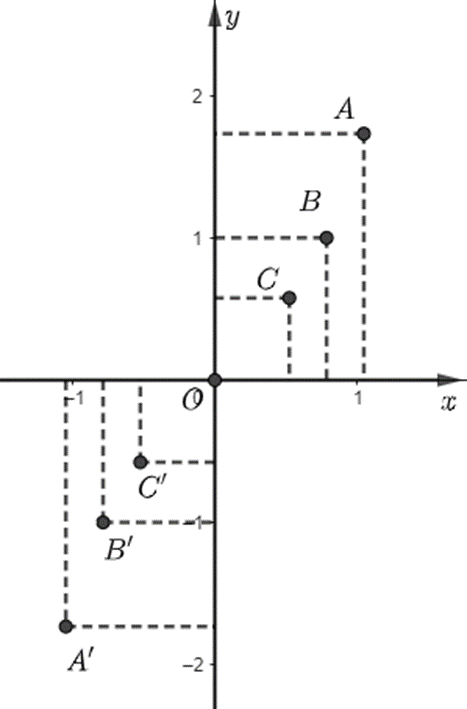
Hoạt động khám phá 6 trang 30 Toán 11 Tập 1: Hoàn thành bảng giá trị sau đây và xác định các điểm tương ứng trên mặt phẳng tọa độ.

x	$-\frac{\pi }{3}$	$-\frac{\pi }{4}$	$-\frac{\pi }{6}$	0	$\frac{\pi }{6}$	$\frac{\pi }{4}$	$\frac{\pi }{3}$
y = tanx	?	?	?	?	?	?	?

Lời giải:

Với $x=-\frac{\pi }{3}$ thì $y=\tan \left(-\frac{\pi }{3}\right)=-\sqrt{3}$. Ta có điểm A'$\left(-\frac{\pi }{3};-\sqrt{3}\right)$.

Với $x=-\frac{\pi }{4}$ thì $y=\tan \left(-\frac{\pi }{4}\right)=-1$. Ta có điểm B'$\left(-\frac{\pi }{4};-1\right)$.

Với $x=-\frac{\pi }{6}$ thì $y=\tan \left(-\frac{\pi }{3}\right)=-\frac{\sqrt{3}}{3}$. Ta có điểm C'$\left(-\frac{\pi }{6};-\frac{\sqrt{3}}{3}\right)$.

Với $x=0$ thì $y=\tan \left(0\right)=0$. Ta có điểm O(0;0).

Với $x=\frac{\pi }{6}$ thì $y=\tan \left(\frac{\pi }{6}\right)=\frac{\sqrt{3}}{3}$. Ta có điểm C$\left(\frac{\pi }{6};\frac{\sqrt{3}}{3}\right)$.

Với $x=\frac{\pi }{4}$ thì $y=\tan \left(\frac{\pi }{4}\right)=1$. Ta có điểm B$\left(\frac{\pi }{4};1\right)$.

Với $x=\frac{\pi }{3}$ thì $y=\tan \left(\frac{\pi }{3}\right)=\sqrt{3}$. Ta có điểm A$\left(\frac{\pi }{3};\sqrt{3}\right)$.

Khi đó ta có bảng:

x	$-\frac{\pi }{3}$	$-\frac{\pi }{4}$	$-\frac{\pi }{6}$	0	$\frac{\pi }{6}$	$\frac{\pi }{4}$	$\frac{\pi }{3}$
y = tanx	$-\sqrt{3}$	-1	$\frac{-\sqrt{3}}{3}$	0	$\frac{\sqrt{3}}{3}$	1	$\sqrt{3}$

Biểu diễn các điểm trên trên mặt phẳng tọa độ ta được:

Lời giải bài tập Toán 11 Bài 4: Hàm số lượng giác và đồ thị Chân trời sáng tạo hay khác:

• Giải Toán 11 trang 25

• Giải Toán 11 trang 27

• Giải Toán 11 trang 28

• Giải Toán 11 trang 32

• Giải Toán 11 trang 33