Giải Toán 11 trang 32 Tập 1 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với Giải Toán 11 trang 32 Tập 1 trong Bài 4: Hàm số lượng giác và đồ thị Toán lớp 11 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 32.

Giải Toán 11 trang 32 Tập 1 Chân trời sáng tạo

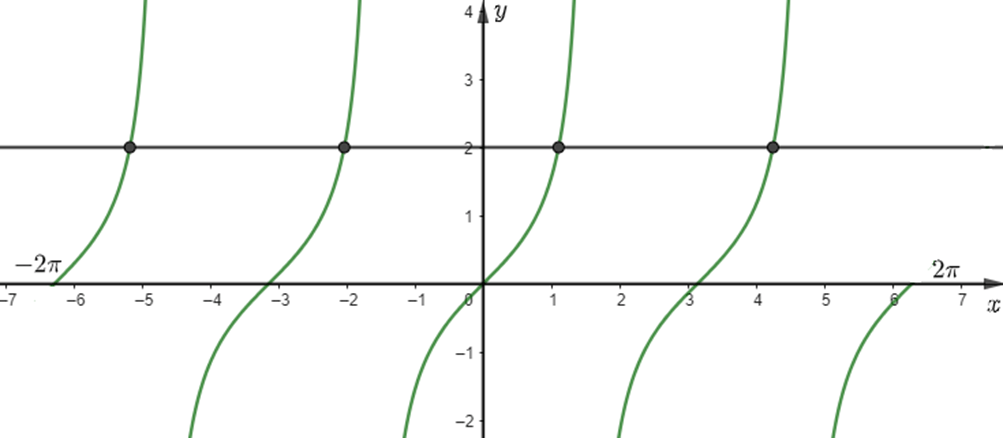
Thực hành 4 trang 32 Toán 11 Tập 1: Có bao nhiêu giá trị x trên đoạn [–2π; 2π] thỏa mãn điều kiện tanx = 2?

Lời giải:

Cách 1: Ta có đồ thị của hàm số trên đoạn [–2π; 2π] là:

Do đó có 4 giá trị x thỏa mãn điều kiện bài toán.

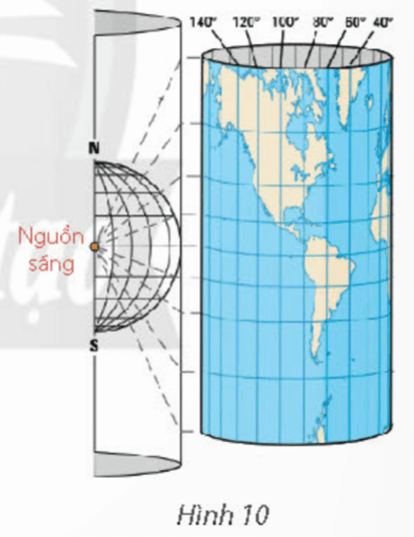
Vận dụng 2 trang 32 Toán 11 Tập 1: Trong địa lí, phép chiếu hình trụ được sử dụng để vẽ một bản đồ phẳng như trong Hình 10. Trên bản đồ phẳng lấy đường xích đạo làm trục hoàng và kinh tuyến 0⁰ làm trục tung. Khi đó tung độ của một điểm có vĩ độ ${\phi }^o$(-90 <$\phi$< 90) được cho bởi hàm số y = 20tan$\left(\frac{\pi }{180}\phi \right)$ (cm). Sử dụng đồ thị hàm số tang, hãy cho biết những điểm ở vĩ độ nào nằm cách xích đạo 20 cm trên bản đồ.

(Theo https://geologyscience.com/geology/types-of-maps/)

Lời giải:

Nội dung đang được cập nhật

Bài 1 trang 32 Toán 11 Tập 1: Các hàm số dưới đây có là hàm số chẵn hay hàm số lẻ không?

a) y = 5sin²x + 1;

b) y = cosx + sinx;

c) y = tan2x.

Lời giải:

a) Xét hàm số: y = 5sin²x + 1, có:

Tập xác định D = ℝ.

Nếu x ∈ D thì – x ∈ D có y( – x) = 5sin²(– x) + 1 = 5sin² x + 1 = y(x).

Vì vậy hàm số này là hàm chẵn.

b) Xét hàm số: y = cosx + sinx

Tập xác định: D = ℝ

Nếu x ∈ D thì – x ∈ D có y( – x) = cos(– x) + sin(– x) = cosx – sin x ≠ y(x).

Vì vậy hàm số này không là hàm chẵn cũng không là hàm lẻ.

c) y = tan2x.

Tập xác định D = $ℝ\backslash \left(\frac{\pi }{4}+k\pi ,k\in \mathbb{Z}\right)$.

Nếu x ∈ D thì – x ∈ D có y( – x) = tan(– 2x) = – tan2x ≠ y(x).

Vì vậy hàm số này là hàm lẻ.

Bài 2 trang 32 Toán 11 Tập 1: Tìm tập xác định của các hàm số sau:

a) $y=\frac{1}{\cos x}$;

b) $\tan \left(x+\frac{\pi }{4}\right)$;

c) $y=\frac{1}{2-{\sin }^{2}x}$.

Lời giải:

a) Điều kiện xác định là: $\text{cos}x\ne 0\iff x\ne \frac{\pi }{2}+k2\pi ,k\in \mathbb{Z}$

Suy ra tập xác định của hàm số $y=\frac{1}{\cos x}$ là: $D=ℝ\backslash \left(\frac{\pi }{2}+k2\pi ,k\in \mathbb{Z}\right)$.

b) Điểu kiện xác định là: $\text{cos}\left(x+\frac{\pi }{4}\right)\ne 0\iff x\ne \frac{\pi }{4}+k2\pi ,k\in \mathbb{Z}$

Suy ra tập xác định của hàm số $y=\tan \left(x+\frac{\pi }{4}\right)$ là: $D=ℝ\backslash \left(\frac{\pi }{4}+k2\pi ,k\in \mathbb{Z}\right)$.

c) Điều kiện xác định là: $2-{\sin }^{2}x\ne 0$

Vì $-1\le x\le 1$ nên $2-{\sin }^{2}x\ne 0$ với mọi x ∈ ℝ.

Suy ra tập xác định của hàm số $y=\frac{1}{2-{\sin }^{2}x}$ là: D = ℝ.

Lời giải bài tập Toán 11 Bài 4: Hàm số lượng giác và đồ thị Chân trời sáng tạo hay khác:

• Giải Toán 11 trang 25

• Giải Toán 11 trang 27

• Giải Toán 11 trang 28

• Giải Toán 11 trang 30

• Giải Toán 11 trang 33