Giải Toán 11 trang 36 Tập 1 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với Giải Toán 11 trang 36 Tập 1 trong Bài 5: Phương trình lượng giác Toán lớp 11 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 36.

Giải Toán 11 trang 36 Tập 1 Chân trời sáng tạo

Thực hành 2 trang 36 Toán 11 Tập 1: Giải các phương trình sau:

a) sinx = $\frac{\sqrt{3}}{2}$;

b) sin(x + 30°) = sin(x + 60°).

Lời giải:

a) sinx = $\frac{\sqrt{3}}{2}$

Vì sin$\frac{\pi }{3}$ = $\frac{\sqrt{3}}{2}$ nên phương trình sinx = $\frac{\sqrt{3}}{2}$= sin$\frac{\pi }{3}$ có các nghiệm là:

$\text{x}=\frac{\pi }{3}+k2\pi$ và $x=\frac{2\pi }{3}+k2\pi$, k ∈ ℤ.

Vậy tập nghiệm của phương trình đã cho là: S = $\left(\frac{\pi }{3}+k2\pi ,\frac{2\pi }{3}+k2\pi ,k\in \mathbb{Z}\right)$.

b) sin(x + 30°) = sin(x + 60°)

⇔ x + 30° = x + 60° + k360° hoặc x + 30° = 360° – x – 60° + k360° (k ∈ ℤ)

⇔ 30° = 60° + k360° (vô lí) hoặc x = 150° + k180° (k ∈ ℤ).

Vậy tập nghiệm của phương trình đã cho là: S = {150° + k180°, k ∈ ℤ}.

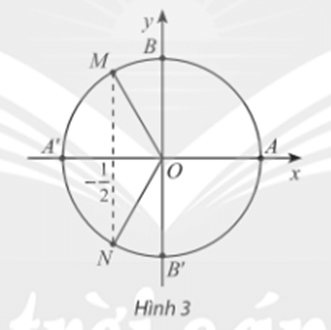
Hoạt động khám phá 3 trang 36 Toán 11 Tập 1: Trong Hình 3, những điểm nào trên đường tròn lượng giác biểu diễn diễn góc lượng giác x có cosx = $-\frac{1}{2}$? Xác định số đo của các góc lượng giác đó.

Lời giải:

Trên đường tròn lượng giác điểm M và N biểu diễn diễn góc lượng giác x có cosx = $-\frac{1}{2}$.

Điểm M là điểm biểu diễn cho các góc lượng giác có số đo là: $\frac{2\pi }{3}+k2\pi ,k\in \mathbb{Z}$.

Điểm N là điểm biểu diễn cho các góc lượng giác có số đo là: $-\frac{2\pi }{3}+k2\pi ,k\in \mathbb{Z}$.

Lời giải bài tập Toán 11 Bài 5: Phương trình lượng giác Chân trời sáng tạo hay khác:

• Giải Toán 11 trang 34

• Giải Toán 11 trang 35

• Giải Toán 11 trang 37

• Giải Toán 11 trang 38

• Giải Toán 11 trang 39

• Giải Toán 11 trang 40

• Giải Toán 11 trang 41