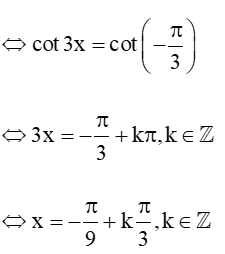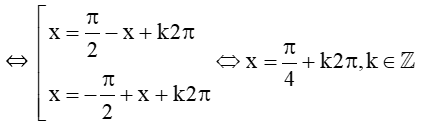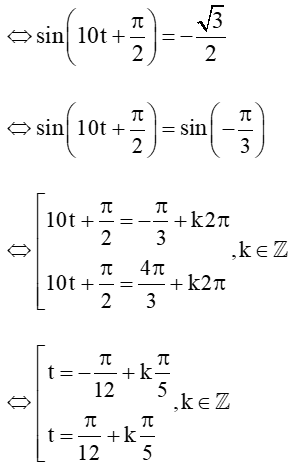Giải Toán 11 trang 41 Tập 1 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với Giải Toán 11 trang 41 Tập 1 trong Bài 5: Phương trình lượng giác Toán lớp 11 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 41.

Giải Toán 11 trang 41 Tập 1 Chân trời sáng tạo

Bài 3 trang 41 Toán 11 Tập 1: Giải các phương trình lượng giác sau:

a) tanx = tan55°;

b) tan$\left(2x+\frac{\pi }{4}\right)$=0.

Lời giải:

a) tanx = tan55° (điều kiện xác định x ≠ 90° + k180°).

⇔ x = 55° + k180°, k ∈ ℤ (thỏa mãn điều kiện)

Vậy tập nghiệm của phương trình S = {55° + k180°, k ∈ ℤ}.

b) tan$\left(2x+\frac{\pi }{4}\right)$=0 (điều kiện xác định $2x+\frac{\pi }{4}\ne \frac{\pi }{2}+k2\pi \iff x\ne \frac{\pi }{8}+k\pi ,k\in \mathbb{Z}$)

$\iff 2x+\frac{\pi }{4}=k\pi ,k\in \mathbb{Z}$

$\iff x=-\frac{\pi }{4}+k\frac{\pi }{2},k\in \mathbb{Z}$ (thỏa mãn điều kiện)

Vậy tập nghiệm của phương trình là S = $\left(-\frac{\pi }{4}+k\frac{\pi }{2},k\in \mathbb{Z}\right)$.

Bài 4 trang 41 Toán 11 Tập 1: Giải các phương trình lượng giác sau:

a) cot$\left(\frac{1}{2}x+\frac{\pi }{4}\right)$= -1;

b) cot3x = $-\frac{\sqrt{3}}{3}$.

Lời giải:

a) cot$\left(\frac{1}{2}x+\frac{\pi }{4}\right)$ = -1 (điểu kiện xác định x # $\frac{\pi }{2}$ + k2$\pi$, k$\in$Z)

$\iff \frac{1}{2}x+\frac{\pi }{4}=-\frac{\pi }{4}+k\pi ,k\in \mathbb{Z}$

$\iff x=-\pi +k2\pi ,k\in \mathbb{Z}$ (thỏa mãn điều kiện)

Vậy tập nghiệm của phương trình là S = $\left(-\pi +k2\pi ,k\in \mathbb{Z}\right)$.

b) cot3x = $-\frac{\sqrt{3}}{3}$ (điểu kiện xác định x # k$\frac{\pi }{3}$, k$\in$Z)

Vậy tập nghiệm của phương trình là S = $\left(-\frac{\pi }{9}+k\frac{\pi }{3},k\in \mathbb{Z}\right)$.

Bài 5 trang 41 Toán 11 Tập 1: Tại các giá trị nào của x thì đồ thị hàm số y = cosx và y = sinx giao nhau?

Lời giải:

Xét phương trình hoành độ giao điểm: sinx = cosx

⇔ cosx = cos$\left(\frac{\pi }{2}-x\right)$

Vậy tập nghiệm của bất phương trình là: S = $\left(\frac{\pi }{4}+k2\pi ,k\in \mathbb{Z}\right)$.

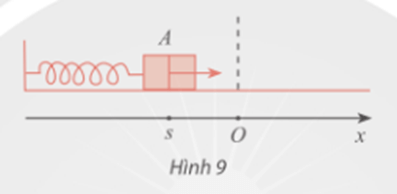
Bài 6 trang 41 Toán 11 Tập 1: Trong Hình 9, khi được kéo ra khỏi vị trí cân bằng ở điểm O và buông tay, lực đàn hồi của lò xo khiến vật A gắn ở đầu của lò xo dao động quanh O. Tọa độ s (cm) của A trên trục Ox vào thời điểm t (giây) sau khi buông tay được xác định bởi công thức s = 10sin$\left(10t+\frac{\pi }{2}\right)$. Vào các thời điểm nào thì s = -5$\sqrt{3}$ cm?

(Theo https://www.britannica.com/science/simple-harmonic-motion )

Lời giải:

Xét phương trình: 10sin$\left(10t+\frac{\pi }{2}\right)$ = -5$\sqrt{3}$

Vậy vào các thời điểm $t=-\frac{\pi }{12}+k\frac{\pi }{5}\left(k\ge 1,k\in \mathbb{Z}\right)$ và $t=\frac{\pi }{12}+k\frac{\pi }{5}\left(k\ge 0,k\in \mathbb{Z}\right)$ thì s = -5$\sqrt{3}$ cm.

Bài 7 trang 41 Toán 11 Tập 1: Trong Hình 10, ngọn đèn hải đăng H cách bờ biển yy’ một khoảng HO = 1km. Đèn xoay ngược chiều kim đồng hồ với tốc độ $\frac{\pi }{10}$ rad/s và chiếu hai luồng ánh sáng về hai phía đối diện nhau. Khi đèn xoay, điểm M mà luồng ánh sáng của hải đăng rọi vào bờ biển chuyển động dọc theo bờ.

(Theo https://www.mnhs.org/splitrock/learn/technology)

a) Ban đầu luồng sáng trùng với đường thẳng HO. Viết hàm số biểu thị tọa độ y_M của điểm M trên trục Oy theo thời gian t.

b) Ngôi nhà N nằm trên bờ biển với tọa độ y_S = – 1 (km). Xác định các thời điểm t mà đèn hải đăng chiếu vào ngôi nhà.

Lời giải:

a) Sau t giây điểm M quét được một góc lượng giác có số đo là: $\alpha =\frac{\pi }{10}t$ rad.

Xét tam giác HOM vuông tại O có:

MO = tanα.1 = tan$\left(\frac{\pi }{10}t\right)$.

Vậy tọa độ y_M = tan$\left(\frac{\pi }{10}t\right)$.

b) Xét tan$\left(\frac{\pi }{10}t\right)$ = -1

$\iff$ tan$\left(\frac{\pi }{10}t\right)$ = tan$\left(-\frac{\pi }{4}\right)$

$\iff$ $\frac{\pi }{10}t$ = $-\frac{\pi }{4}$ + k$\pi$, k$\in$Z

$\iff$ t = -2,5 + 10k, k$\in$Z

Vì t ≥ 0 nên tại các thời điểm t = -2,5 + 10k, k$\in$Z, k$\ge$1 thì đèn hải đăng chiếu vào ngôi nhà.

Lời giải bài tập Toán 11 Bài 5: Phương trình lượng giác Chân trời sáng tạo hay khác:

• Giải Toán 11 trang 34

• Giải Toán 11 trang 35

• Giải Toán 11 trang 36

• Giải Toán 11 trang 37

• Giải Toán 11 trang 38

• Giải Toán 11 trang 39

• Giải Toán 11 trang 40