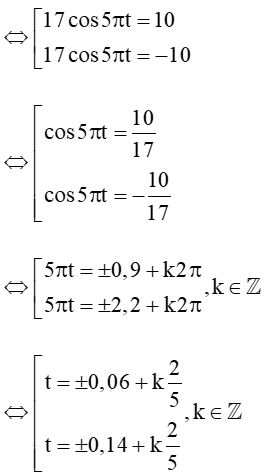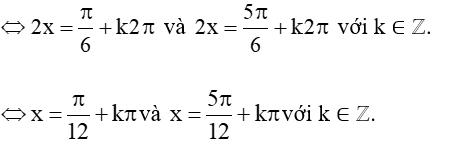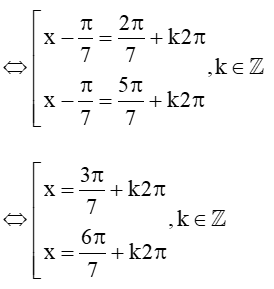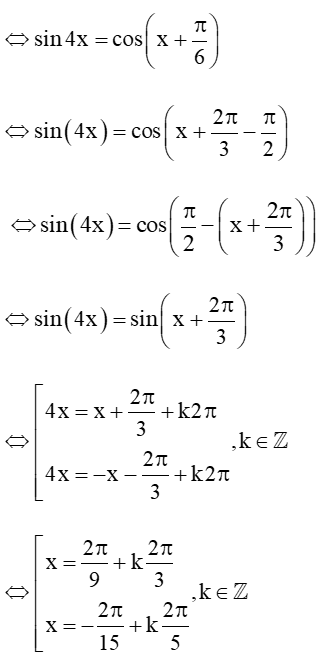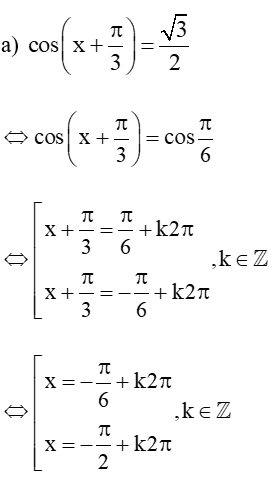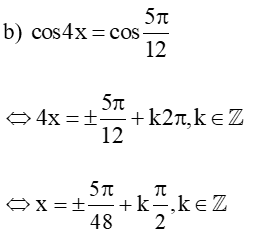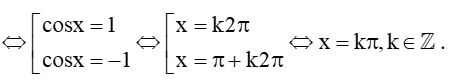Giải Toán 11 trang 40 Tập 1 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với Giải Toán 11 trang 40 Tập 1 trong Bài 5: Phương trình lượng giác Toán lớp 11 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 40.

Giải Toán 11 trang 40 Tập 1 Chân trời sáng tạo

Thực hành 6 trang 40 Toán 11 Tập 1: Sử dụng máy tính cầm tay để giải các phương trình sau:

a) cosx = 0,4;

b) tanx = $\sqrt{3}$.

Lời giải:

a) Sử dụng máy tính cầm tay ta có: cos1,16 ≈ 0,4 nên cosx = cos1,16 do đó các nghiệm của phương trình là x = 1,16 + k2π và x = – 1,16 + k2π với k ∈ ℤ.

Vậy tập nghiệm của phương trình là S = {1,16 + k2π; – 1,16 + k2π, k ∈ ℤ}.

b) Sử dụng máy tính cầm tay ta có: tan$\frac{\pi }{3}$ = $\sqrt{3}$ nên tanx = tan$\frac{\pi }{3}$ do đó các nghiệm của phương trình là x = $\frac{\pi }{3}$ + k$\pi$ với k ∈ ℤ.

Vậy tập nghiệm của phương trình là S = $\left(\frac{\pi }{3}+k\pi ,k\in \mathbb{Z}\right)$.

Vận dụng trang 40 Toán 11 Tập 1: Quay lại bài toán khởi động, phương trình chuyển động của bóng đầu trục bàn đạp là x = 17cos5πt (cm) với t được đo bằng giây. Xác định các thời điểm t mà tại đó độ dài bóng |x| bằng 10 cm. Làm tròn kết quả đến hàng phần mười.

Lời giải:

Xét phương trình |17cos5πt| = 10

Độ dài bóng |x| bằng 10 cm tại các thời điểm t = $\pm$0,06 +k$\frac{2}{5}$, t = $\pm$0,14 + k$\frac{2}{5}$ (k$\in$Z).

Bài 1 trang 40 Toán 11 Tập 1: Giải các phương trình lượng giác sau:

a) sin2x = $\frac{1}{2}$;

b) sin$\left(x-\frac{\pi }{7}\right)$ = sin$\frac{2\pi }{7}$;

c) sin4x - cos$\left(x+\frac{\pi }{6}\right)$ = 0.

Lời giải:

a) Vì sin$\frac{\pi }{6}$ = $\frac{1}{2}$ nên ta có phương trình sin2x = sin$\frac{\pi }{6}$

Vậy tập nghiệm của phương trình là: S = $\left(\frac{\pi }{12}+k\pi ,\frac{5\pi }{12}+k\pi ,k\in \mathbb{Z}\right)$.

b) sin$\left(x-\frac{\pi }{7}\right)$= sin$\frac{2\pi }{7}$

Vậy tập nghiệm của phương trình là: S = $\left(\frac{3\pi }{7}+k2\pi ;\frac{6\pi }{7}+k2\pi ,k\in \mathbb{Z}\right)$.

c) sin4x - cos$\left(x+\frac{\pi }{6}\right)$ = 0

Vậy tập nghiệm của phương trình là: S = $\left(\frac{2\pi }{9}+k\frac{2\pi }{3};-\frac{2\pi }{15}+k\frac{2\pi }{5},k\in \mathbb{Z}\right)$.

Bài 2 trang 40 Toán 11 Tập 1: Giải các phương trình lượng giác sau:

a) cos$\left(x+\frac{\pi }{3}\right)=\frac{\sqrt{3}}{2}$;

b) cos4x = cos$\frac{5\pi }{12}$;

c) cos²x = 1.

Lời giải:

Vậy tập nghiệm của phương trình là: S = $\left(-\frac{\pi }{6}+k2\pi ;-\frac{\pi }{2}+k2\pi ,k\in \mathbb{Z}\right)$.

Vậy tập nghiệm của phương trình là: S = $\left(\pm \frac{5\pi }{48}+k\frac{\pi }{2},k\in \mathbb{Z}\right)$.

c) cos²x = 1

Vậy tập nghiệm của phương trình là: S = {k$\pi$, k$\in$Z}.

Lời giải bài tập Toán 11 Bài 5: Phương trình lượng giác Chân trời sáng tạo hay khác:

• Giải Toán 11 trang 34

• Giải Toán 11 trang 35

• Giải Toán 11 trang 36

• Giải Toán 11 trang 37

• Giải Toán 11 trang 38

• Giải Toán 11 trang 39

• Giải Toán 11 trang 41