Giải Toán 11 trang 84 Tập 1 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với Giải Toán 11 trang 84 Tập 1 trong Bài 3: Hàm số liên tục Toán lớp 11 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 84.

Giải Toán 11 trang 84 Tập 1 Chân trời sáng tạo

Thực hành 5 trang 84 Toán 11 Tập 1: Xét tính liên tục của hàm số:

a) y = $\sqrt{x^2+1}$ + 3 - x;

b) y = $\frac{x^2-1}{x}$.cos x.

Lời giải:

a) Đặt y = f(x) = $\sqrt{x^2+1}$ + 3 - x

Tập xác định của hàm số D = ℝ.

Khi đó $\underset{x\to x_0}{\lim }f\left(x\right)=\underset{x\to x_0}{\lim }\left(\sqrt{x^2+1}+3-x\right)=\sqrt{x_0^2+1}+3-x_0=f\left(x_0\right)$.

Vậy hàm số liên tục trên ℝ.

b) Đặt y = g(x) = $\frac{x^2-1}{x}$.cos x.

Tập xác định của hàm số D = ℝ\{0}.

Trên các khoảng (– ∞; 0) và (0; +∞) ta thấy hàm số $y=\frac{x^2-1}{x}$ và y = cos x liên tục.

Vậy hàm số đã cho liên tục trại mọi điểm x₀ ≠ 0.

Vận dụng 3 trang 84 Toán 11 Tập 1: Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) tâm O, bán kính bằng 1. Một đường thẳng d thay đổi, luôn vuông góc với trục hoành, cắt trục hoành tại điểm M có hoành độ x (– 1 < x < 1) và cắt đường tròn (C) tại các điểm N và P (xem Hình 6).

a) Viết biểu thức S(x) biểu thị diện tích của tam giác ONP.

b) Hàm số y = S(x) có liên tục trên (– 1; 1) không? Giải thích.

c) Tìm các giới hạn $\underset{x\to 1^{-}}{\lim }S\left(x\right)$ và $\underset{x\to -1^{+}}{\lim }S\left(x\right)$.

Lời giải:

a) Xét tam giác OMN vuông tại M có:

MN = $\sqrt{O{N}^2-O{M}^2}=\sqrt{1-x^2}$

$\Rightarrow NP=2\sqrt{1-x^2}$

Diện tích của tam giác ONP là:

S(x) = $\frac{1}{2}$.NP.OM = $\frac{1}{2}$.2.$\sqrt{1-x^2}$.x = x$\sqrt{1-x^2}$

b) Trên (– 1; 1) hàm số y = $\sqrt{1-x^2}$ xác định và liên tục và hàm số y = x liên tục.

Do đó hàm số S(x) liên tục trên (– 1; 1).

c) Ta có:

$\underset{x\to -1^{+}}{\text{lim}}\text{S}\left(x\right)=\underset{x\to -1^{+}}{\text{lim}}\left(\sqrt{1-x^2}.x\right)=0$

$\underset{x\to 1^{-}}{\text{lim}}\text{S}\left(x\right)=\underset{x\to 1^{-}}{\text{lim}}\left(\sqrt{1-x^2}.x\right)=0$.

Bài 1 trang 84 Toán 11 Tập 1: Xét tính liên tục của hàm số sau:

a) f(x) = 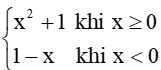tại điểm x = 0;

b) f(x) = 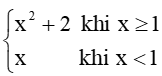tại điểm x = 1.

Lời giải:

a) Tại x = 0, ta có:

$\underset{x\to 0^{+}}{\lim }f\left(x\right)=\underset{x\to 0^{+}}{\lim }\left(x^2+1\right)=1$;

$\underset{x\to 0^{-}}{\lim }f\left(x\right)=\underset{x\to 0^{-}}{\lim }\left(1-x\right)=1$.

Suy ra $\underset{x\to 0^{+}}{\lim }f\left(x\right)=\underset{x\to 0^{-}}{\lim }f\left(x\right)=1$. Do đó $\underset{x\to 0}{\lim }f\left(x\right)=1$

Mà f(0) = 0² + 1 = 1 nên $\underset{x\to 0}{\lim }f\left(x\right)=f\left(0\right)=1$.

Vậy hàm số đã cho liên tục tại điểm x = 0.

b) Tại x = 1 ta có:

$\underset{x\to 1^{+}}{\lim }f\left(x\right)=\underset{x\to 1^{+}}{\lim }\left(x^2+2\right)=3$;

$\underset{x\to 1^{-}}{\lim }f\left(x\right)=\underset{x\to 1^{-}}{\lim }x=1$.

Suy ra $\underset{x\to 1^{+}}{\lim }f\left(x\right)\ne \underset{x\to 1^{-}}{\lim }f\left(x\right)$. Do đó không tồn tại $\underset{x\to 1}{\lim }f\left(x\right)$.

Vậy hàm số không liên tục tại x = 1.

Bài 2 trang 84 Toán 11 Tập 1: Cho hàm số f(x) = 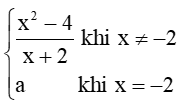. Tìm a để hàm số f(x) liên tục trên ℝ.

Lời giải:

Ta có:

$\underset{x\to -2}{\lim }f\left(x\right)=\underset{x\to -2}{\lim }\frac{x^2-4}{x+2}=\underset{x\to -2}{\lim }\frac{\left(x-2\right)\left(x+2\right)}{x+2}=\underset{x\to -2}{\lim }\left(x-2\right)=-4$.

f(-2) = a.

Để hàm số f(x) liên tục trên ℝ thì hàm số liên tục tại x = – 2

$\iff \underset{x\to -2}{\lim }f\left(x\right)$= f(-2)

$\iff$a = -4

Vậy a = – 4 thì hàm số đã cho liên tục trên ℝ.

Lời giải bài tập Toán 11 Bài 3: Hàm số liên tục Chân trời sáng tạo hay khác:

• Giải Toán 11 trang 80

• Giải Toán 11 trang 81

• Giải Toán 11 trang 82

• Giải Toán 11 trang 83

• Giải Toán 11 trang 85