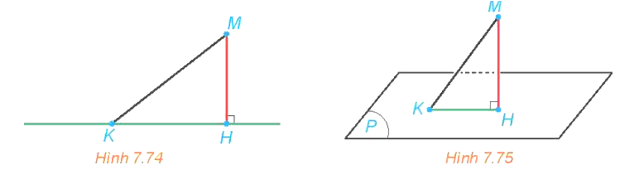
b) Các cặp cạnh đối diện trong tứ diện ABCD đều vuông góc với nhau.
Câu hỏi:
b) Các cặp cạnh đối diện trong tứ diện ABCD đều vuông góc với nhau.
Trả lời:
b) Vì AB ^ (DCM) nên AB ^ CD.
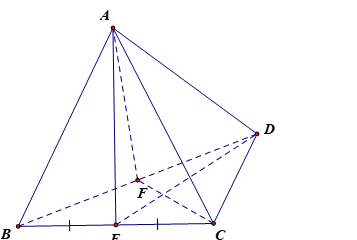
Gọi E là trung điểm của BC.
Xét tam giác ABC có AB = AC = a nên tam giác ABC cân tại A mà AE là trung tuyến nên AE đồng thời là đường cao hay AE ^ BC.
Xét tam giác BDC có BD = CD = a nên tam giác BCD cân tại D mà DE là trung tuyến nên DE đồng thời là đường cao hay DE ^ BC.
Có AE ^ BC và DE ^ BC nên BC ^ (ADE), suy ra BC ^ AD.
Gọi F là trung điểm của BD.
Xét tam giác ADB có AB = AD = a nên tam giác ADB cân tại A mà AF là trung tuyến nên AF đồng thời là đường cao hay AF ^ BD.
Xét tam giác BCD có BC = CD = a nên tam giác BCD cân tại C mà CF là trung tuyến nên CF đồng thời là đường cao hay CF ^ BD.
Vì AF ^ BD và CF ^ BD nên BD ^ (ACF), suy ra BD ^ AC.