Cho hình chóp S.ABCD có đáy là một hình vuông cạnh a, mặt bên SAD là một tam giác đều và (SAD) ^ (ABCD). a) Tính chiều cao của hình chóp.
Câu hỏi:
Cho hình chóp S.ABCD có đáy là một hình vuông cạnh a, mặt bên SAD là một tam giác đều và (SAD) ^ (ABCD).
a) Tính chiều cao của hình chóp.
Trả lời:
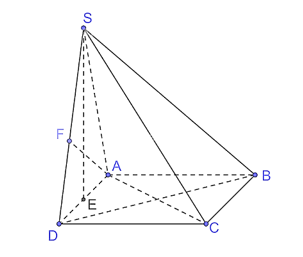
a) Kẻ SE ^ AD tại E.
Vì (SAD) ^ (ABCD), (SAD) Ç (ABCD) = AD mà SE ^ AD nên SE ^ (ABCD).
Vì tam giác SAD là tam giác đều cạnh a nên .
Vậy chiều cao của hình chóp bằng .