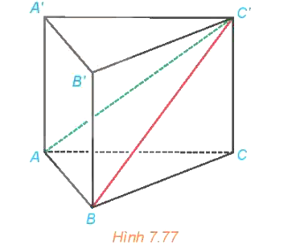
b) Xác định đường vuông góc chung và tính khoảng cách giữa AC và B'D'.
Câu hỏi:
b) Xác định đường vuông góc chung và tính khoảng cách giữa AC và B'D'.
Trả lời:
b) Gọi O là giao điểm của AC và BD, O' là giao điểm của A'C' và B'D'.
Do ABCD là hình chữ nhật nên O là trung điểm của AC, BD và A'B'C'D' là hình chữ nhật nên O' là trung điểm của A'C' và B'D'.
Có AA' // CC' và AA' = CC' (do chúng cùng song song và bằng BB’) nên AA'C'C là hình bình hành mà AA' ^ (ABCD) nên AA' ^ AC. Do đó AA'C'C là hình chữ nhật.
Do AA'C'C là hình chữ nhật và O là trung điểm của AC, O' là trung điểm của A'C' nên OO' ^ AC và OO' = AA' = a.
Có BB' // DD' và BB' = DD' (do chúng cùng song song và bằng AA') nên BB'D'D là hình bình hành mà BB' ^ (ABCD) nên BB' ^ BD. Do đó BB'D'D là hình chữ nhật.
Vì BB'D'D là hình chữ nhật và O là trung điểm của BD, O' là trung điểm của B'D' nên OO' ^ B'D'.
Vì OO' ^ AC và OO' ^ B'D' nên OO' là đường vuông góc chung của AC và B'D'.
Khi đó d(AC, B'D') = OO' = a.