Câu hỏi:
Xét hàm số \(f\left( x \right) = \frac{1}{{{x^2}}}\) có đồ thị như Hình 5.6.
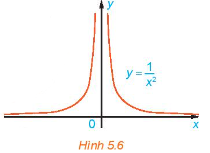
Cho \({x_n} = \frac{1}{n}\), chứng tỏ rằng f(xn) ⟶ +∞.
Trả lời:
Lời giải:
Ta có: \({x_n} = \frac{1}{n}\), do đó \(f\left( {{x_n}} \right) = \frac{1}{{x_n^2}} = \frac{1}{{{{\left( {\frac{1}{n}} \right)}^2}}} = {n^2}\).
Vì n ⟶ +∞ nên \({x_n} = \frac{1}{n} \to 0\) và f(xn) ⟶ +∞.
Câu 1:
Trong Thuyết tương đối của Einstein, khối lượng của vật chuyển động với vận tốc v cho bởi công thức
\(m = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\),
trong đó m0 là khối lượng của vật khi nó đứng yên, c là vận tốc ánh sáng. Chuyện gì xảy ra với khối lượng của vật khi vận tốc của vật gần với vận tốc ánh sáng?
Câu 2:
Cho hàm số \(f\left( x \right) = \frac{{4 - {x^2}}}{{x - 2}}\).
a) Tìm tập xác định của hàm số f(x).
b) Cho dãy số \({x_n} = \frac{{2n + 1}}{n}\). Rút gọn f(xn) và tính giới hạn của dãy (un) với un = f(xn).
c) Với dãy số (xn) bất kì sao cho xn ≠ 2 và xn ⟶ 2, tính f(xn) và tìm \(\mathop {\lim }\limits_{n \to + \infty } f\left( {{x_n}} \right)\).
Câu 4:
Cho hàm số \(f\left( x \right) = \frac{{\left| {x - 1} \right|}}{{x - 1}}\).
a) Cho \({x_n} = 1 - \frac{1}{{n + 1}}\) và \({x'_n} = 1 + \frac{1}{n}\). Tính yn = f(xn) và y'n = f(x'n).
b) Tìm giới hạn của các dãy số (yn) và (y'n).
c) Cho các dãy số (xn) và (x'n) bất kì sao cho xn < 1 < x'n và xn ⟶ 1, x'n ⟶ 1, tính \(\mathop {\lim }\limits_{n \to + \infty } f\left( {{x_n}} \right)\) và \[\mathop {\lim }\limits_{n \to + \infty } f\left( {{{x'}_n}} \right)\].
Câu 5:
Câu 6:
Tính các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to 0} \frac{2}{{\left| x \right|}}\);
b) \(\mathop {\lim }\limits_{x \to {2^ - }} \frac{1}{{\sqrt {2 - x} }}\).
Câu 7:
Câu 8:
Cho hai hàm số \(f\left( x \right) = \frac{{{x^2} - 1}}{{x - 1}}\) và g(x) = x + 1. Khẳng định nào sau đây là đúng?
a) f(x) = g(x);
b) \(\mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} g\left( x \right)\).
