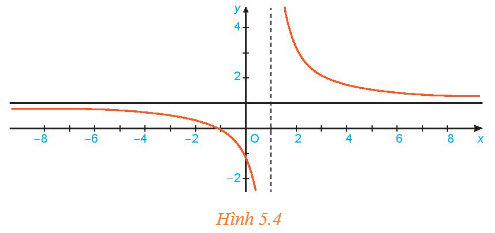
Cho hàm số f( x ) = | x - 1|/x - 1. a) Cho xn = 1 - 1/n + 1 và x'n = 1 + 1/n. Tính yn = f(xn) và y'n = f(x'n). b) Tìm giới hạn của các dãy số (yn) và (y'n). c) Cho các dãy số (xn) và (x'n)
Câu hỏi:
Cho hàm số \(f\left( x \right) = \frac{{\left| {x - 1} \right|}}{{x - 1}}\).
a) Cho \({x_n} = 1 - \frac{1}{{n + 1}}\) và \({x'_n} = 1 + \frac{1}{n}\). Tính yn = f(xn) và y'n = f(x'n).
b) Tìm giới hạn của các dãy số (yn) và (y'n).
c) Cho các dãy số (xn) và (x'n) bất kì sao cho xn < 1 < x'n và xn ⟶ 1, x'n ⟶ 1, tính \(\mathop {\lim }\limits_{n \to + \infty } f\left( {{x_n}} \right)\) và \[\mathop {\lim }\limits_{n \to + \infty } f\left( {{{x'}_n}} \right)\].
Trả lời:
Lời giải:
a) Ta có: \({x_n} = 1 - \frac{1}{{n + 1}} < 1\) với mọi n > 0 \( \Rightarrow {x_n} - 1 < 0\) với mọi n > 0.
Do đó, \({y_n} = f\left( {{x_n}} \right) = \frac{{\left| {{x_n} - 1} \right|}}{{{x_n} - 1}}\)\( = \frac{{ - \left( {{x_n} - 1} \right)}}{{{x_n} - 1}} = - 1\).
Ta cũng có: \({x'_n} = 1 + \frac{1}{n} > 1\) với mọi n > 0 ⇒ x'n – 1 > 0 với mọi n > 0.
Do đó, \({y'_n} = f\left( {{{x'}_n}} \right) = \frac{{\left| {{{x'}_n} - 1} \right|}}{{{{x'}_n} - 1}}\)\( = \frac{{{{x'}_n} - 1}}{{{{x'}_n} - 1}} = 1\).
b) Ta có \(\mathop {\lim }\limits_{n \to + \infty } {y_n} = \mathop {\lim }\limits_{n \to + \infty } \left( { - 1} \right) = - 1\); \(\mathop {\lim }\limits_{n \to + \infty } {y'_n} = \mathop {\lim }\limits_{n \to + \infty } 1 = 1\).
c) Ta có: \(f\left( x \right) = \frac{{\left| {x - 1} \right|}}{{x - 1}}\)\( = \left\{ \begin{array}{l}\frac{{x - 1}}{{x - 1}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,n\^e 'u\,\,x - 1 > 0\,\,\,\,\,\\\frac{{ - \left( {x - 1} \right)}}{{x - 1}}\,\,\,\,\,\,\,\,n\^e 'u\,\,x - 1 < 0\end{array} \right.\)\( = \left\{ \begin{array}{l}1\,\,\,\,\,\,\,\,n\^e 'u\,\,x - 1 > 0\,\,\,\,\,\\ - 1\,\,\,\,n\^e 'u\,\,x - 1 < 0\end{array} \right.\)
Vì xn < 1 < x'n, suy ra xn – 1 < 0 và x'n – 1 > 0 với mọi n.
Do đó, f(xn) = – 1 và f(x'n) = 1.
Vậy \(\mathop {\lim }\limits_{n \to + \infty } f\left( {{x_n}} \right)\) = – 1 và \[\mathop {\lim }\limits_{n \to + \infty } f\left( {{{x'}_n}} \right)\] = 1.