Bài 5 trang 14 Toán 12 Tập 1 Cánh diều
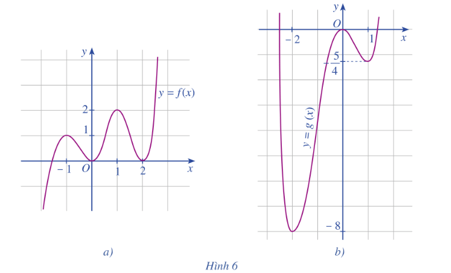
: Cho hai hàm số y = f(x), y = g(x) có đồ thị lần lượt được cho ở Hình 6a, Hình 6b. Nêu khoảng đồng biến, nghịch biến và điểm cực trị của mỗi hàm số đó.
Giải Toán 12 Bài 1: Tính đơn điệu của hàm số - Cánh diều
Bài 5 trang 14 Toán 12 Tập 1: : Cho hai hàm số y = f(x), y = g(x) có đồ thị lần lượt được cho ở Hình 6a, Hình 6b. Nêu khoảng đồng biến, nghịch biến và điểm cực trị của mỗi hàm số đó.
Lời giải:
● Hình 6a:
– Khoảng đồng biến, nghịch biến:
Quan sát hình vẽ ta thấy:
+ Trên các khoảng (– ∞; – 1), (0; 1), (2; + ∞), đồ thị hàm số y = f(x) đi lên từ trái qua phải, do đó hàm số y = f(x) đồng biến trên mỗi khoảng (– ∞; – 1), (0; 1), (2; + ∞).
+ Trên các khoảng (– 1; 0), (1; 2), đồ thị hàm số y = f(x) đi xuống từ trái qua phải, do đó hàm số y = f(x) nghịch biến trên mỗi khoảng (– 1; 0) và (1; 2).
– Điểm cực trị:
+ Xét khoảng (– ∞; 0) chứa điểm x = – 1. Quan sát đồ thị hàm số y = f(x) ở Hình 6a, ta thấy f(x) < f(– 1) với mọi x ∈ (– ∞; 0) và x ≠ – 1. Do đó, x = – 1 là một điểm cực đại của hàm số y = f(x).
Tương tự, ta thấy f(x) < f(1) với mọi x ∈ (0; 2) và x ≠ 1. Do đó, x = 1 là một điểm cực đại của hàm số y = f(x).
+ Xét khoảng (– 1; 1) chứa điểm x = 0. Quan sát đồ thị hàm số ta thấy f(x) > f(0) với mọi x ∈ (– 1; 1) và x ≠ 0. Do đó, x = 0 là một điểm cực tiểu của hàm số y = f(x).
Tương tự, ta thấy f(x) > f(2) với mọi x ∈ (1; + ∞) và x ≠ 2. Vậy x = 2 là một điểm cực tiểu của hàm số y = f(x).
● Hình 6b:
– Khoảng đồng biến, nghịch biến:
Quan sát hình vẽ ta thấy:
+ Trên các khoảng (– 2; 0), (1; + ∞), đồ thị hàm số y = g(x) đi lên từ trái qua phải nên hàm số này đồng biến trên mỗi khoảng (– 2; 0) và (1; + ∞).
+ Trên các khoảng (– ∞; – 2), (0; 1), đồ thị hàm số y = g(x) đi xuống từ trái qua phải nên hàm số này nghịch biến trên mỗi khoảng (– ∞; – 2) và (0; 1).
– Điểm cực trị:
+ Xét khoảng (– ∞; 0) chứa điểm x = – 2. Quan sát đồ thị hàm số y = g(x) ở Hình 6b ta thấy g(x) > g(– 2) với mọi x ∈ (– ∞; 0) và x ≠ – 2. Vậy x = – 2 là một điểm cực tiểu của hàm số y = g(x).
Tương tự, ta thấy g(x) > g(1) với mọi x ∈ (0; + ∞) và x ≠ 1. Do đó, x = 1 là một điểm cực tiểu của hàm số y = g(x).
+ Xét khoảng (– 2; 1) chứa điểm x = 0. Quan sát đồ thị hàm số y = g(x) ở Hình 6b ta thấy g(x) < g(0) với mọi x ∈ (– 2; 1) và x ≠ 0. Do đó, x = 0 là điểm cực đại của hàm số y = g(x).
Lời giải bài tập Toán 12 Bài 1: Tính đơn điệu của hàm số hay, chi tiết khác:
Luyện tập 1 trang 6 Toán 12 Tập 1: Xét dấu y' rồi tìm khoảng đồng biến, nghịch biến của hàm số ....
Luyện tập 2 trang 7 Toán 12 Tập 1: Tìm các khoảng đơn điệu của hàm số y = x4 + 2x2 – 3.....
Hoạt động 2 trang 7 Toán 12 Tập 1: Xác định tính đồng biến, nghịch biến của hàm số f(x) = x3...
Luyện tập 4 trang 8 Toán 12 Tập 1: Tìm các khoảng đơn điệu của hàm số ....