Hoạt động 2 trang 86 Toán 12 Tập 1 Cánh diều

---

Xét mẫu số liệu ghép nhóm cho bởi .

Giải Toán 12 Bài 1: Khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm - Cánh diều

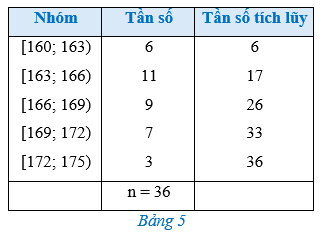
Hoạt động 2 trang 86 Toán 12 Tập 1: Xét mẫu số liệu ghép nhóm cho bởi Bảng 5.

a)

- Nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng $\frac{n}{4}=\frac{36}{4}=9$ có đúng không?

- Tìm đầu mút trái s, độ dài h, tần số n₂ của nhóm 2; tần số tích lũy cf₁ của nhóm 1. Sau đó, hãy tính tứ phân vị thứ nhất Q_1­ của mẫu số liệu đã cho theo công thức sau:

$Q_1=s+\left(\frac{9-c{f}_1}{n_2}\right)\cdot h$.

b)

- Nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng $\frac{n}{2}=\frac{36}{2}=18$ có đúng không?

- Tìm đầu mút trái r, độ dài d, tần số n₃ của nhóm 3; tần số tích lũy cf₂ của nhóm 2. Sau đó, hãy tính tứ phân vị thứ hai Q₂ của mẫu số liệu đã cho theo công thức sau:

$Q_2=r+\left(\frac{18-c{f}_2}{n_3}\right)\cdot d$.

c)

- Nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng $\frac{3n}{4}=\frac{3\cdot 36}{4}=27$ có đúng không?

- Tìm đầu mút trái t, độ dài l, tần số n₄ của nhóm 4; tần số tích lũy cf₃ của nhóm 3. Sau đó, hãy tính tứ phân vị thứ hai Q₃ của mẫu số liệu đã cho theo công thức sau:

$Q_2=t+\left(\frac{27-c{f}_3}{n_4}\right)\cdot l$.

d) Tìm hiệu Q₃ – Q₁.

Lời giải:

a) - Tần số tích lũy của nhóm 1 là 6 < 9, tần số tích lũy của nhóm 2 là 17 > 9.

Vậy nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng $\frac{n}{4}=\frac{36}{4}=9$.

- Nhóm 2 có đầu mút trái s = 163, độ dài h = 163 – 160 = 3, tần số n₂ = 11; tần số tích lũy của nhóm 1 là cf₁ = 6.

Tứ phân vị thứ nhất Q₁ của mẫu số liệu đã cho là

$Q_1=s+\left(\frac{9-c{f}_1}{n_2}\right)\cdot h=163+\left(\frac{9-6}{11}\right)\cdot 3=\frac{1802}{11}\approx 163,82$.

b) - Tần số tích lũy của nhóm 1 là 6 < 18, tần số tích lũy của nhóm 2 là 17 < 18, tần số tích lũy của nhóm 3 là 26 > 18.

Vậy nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng $\frac{n}{2}=\frac{36}{2}=18$.

- Nhóm 3 có đầu mút trái r = 166, độ dài d = 169 – 166 = 3, tần số n₃ = 9; tần số tích lũy của nhóm 2 là cf₂ = 17.

Tứ phân vị thứ hai Q₂ của mẫu số liệu đã cho là

$Q_2=r+\left(\frac{18-c{f}_2}{n_3}\right)\cdot d=166+\left(\frac{18-17}{9}\right)\cdot 3=\frac{499}{3}\approx 166,33$.

c) - Tần số tích lũy của nhóm 1 là 6 < 27, tần số tích lũy của nhóm 2 là 17 < 27, tần số tích lũy của nhóm 3 là 26 < 27, tần số tích lũy của nhóm 4 là 33 > 27.

Vậy nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng $\frac{3n}{4}=\frac{3\cdot 36}{4}=27$.

- Nhóm 4 có đầu mút trái t = 169, độ dài l = 172 – 169 = 3, tần số n₄ = 7; tần số tích lũy của nhóm 3 là cf₃ = 26.

Tứ phân vị thứ ba Q₃ của mẫu số liệu đã cho là

$Q_3=t+\left(\frac{27-c{f}_3}{n_4}\right)\cdot l=169+\left(\frac{27-26}{7}\right)\cdot 3=\frac{1186}{7}\approx 169,43$.

d) Ta có Q₃ – Q₁ = $\frac{1186}{7}-\frac{1802}{11}=\frac{432}{77}$ ≈ 5,61.

Lời giải bài tập Toán 12 Bài 1: Khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm hay, chi tiết khác:

• Câu hỏi khởi động trang 84 Toán 12 Tập 1: Bảng 1 là bảng tần số ghép nhóm biểu diễn mẫu số liệu ghi lại năng suất lúa (đơn vị: tạ/ha) ....

• Hoạt động 1 trang 84 Toán 12 Tập 1: Xét mẫu số liệu ghép nhóm cho bởi Bảng 2 ....

• Luyện tập 1 trang 85 Toán 12 Tập 1: Tính khoảng biến thiên của mẫu số liệu ghép nhóm cho bởi Bảng 1 trong phần mở đầu ....

• Luyện tập 2 trang 87 Toán 12 Tập 1: Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm được cho bởi Bảng 1 trong phần mở đầu ....

• Bài 1 trang 88 Toán 12 Tập 1: Bảng 8 biểu diễn mẫu số liệu ghép nhóm về số tiền (đơn vị: nghìn đồng) mà 60 khách hàng mua sách ....

• Bài 2 trang 88 Toán 12 Tập 1: Bảng 9 biểu diễn mẫu số liệu ghép nhóm thống kê mức lương của một công ty (đơn vị: triệu đồng) ....

• Bài 3 trang 88 Toán 12 Tập 1: Bảng 10 biểu diễn mẫu số liệu ghép nhóm về độ tuổi của cư dân trong một khu phố ....