Luyện tập 2 trang 87 Toán 12 Tập 1 Cánh diều

Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm được cho bởi trong phần mở đầu.

Giải Toán 12 Bài 1: Khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm - Cánh diều

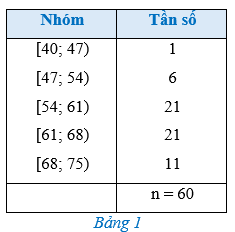
Luyện tập 2 trang 87 Toán 12 Tập 1: Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm được cho bởi Bảng 1 trong phần mở đầu.

Luyện tập 2 trang 87 Toán 12 Cánh diều Tập 1

Lời giải:

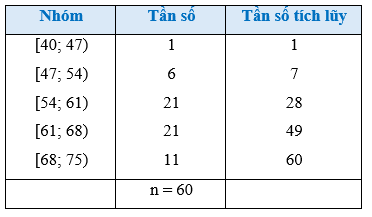
Từ Bảng 1 ta có bảng sau:

Luyện tập 2 trang 87 Toán 12 Cánh diều Tập 1

Số phần tử của mẫu là n = 60.

- Ta có: $\frac{n}{4} = \frac{60}{4} = 15$ mà 7 < 15 < 28. Suy ra nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 15. Xét nhóm 3 là nhóm [54; 61) có s = 54; h = 7; n₃ = 21 và nhóm 2 là nhóm [47; 54) có cf₂ = 7.

Áp dụng công thức, ta có tứ phân vị thứ nhất là

$Q_{1} = 54 + (\frac{15 - 7}{21}) \cdot 7 = \frac{170}{3}$ (tạ/ha).

- Ta có: $\frac{3 n}{4} = \frac{3 \cdot 60}{4} = 45$ mà 28 < 45 < 49. Suy ra nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 45. Xét nhóm 4 là nhóm [61; 68) có t = 61; l = 7; n₄ = 21 và nhóm 3 là nhóm [54; 61) có cf₃ = 28.

Áp dụng công thức, ta có tứ phân vị thứ ba là

$Q_{3} = 61 + (\frac{45 - 28}{21}) \cdot 7 = \frac{200}{3}$ (tạ/ha).

Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho là:

∆_Q = Q₃ – Q₁ = $\frac{200}{3} - \frac{170}{3}$ = 10 (tạ/ha).

Lời giải bài tập Toán 12 Bài 1: Khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm hay, chi tiết khác:

Xem thêm lời giải bài tập Toán lớp 12 Cánh diều hay, chi tiết khác:

❮ Bài trước Bài sau ❯