Bài 14 trang 38 Toán 12 Tập 1 Chân trời sáng tạo

---

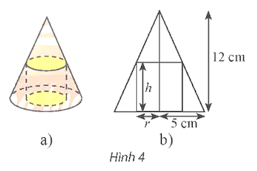
Cho một hình trụ nội tiếp trong hình nón có chiều cao bằng 12 cm và bán kính đáy bằng 5 cm (Hình 4a). Người ta cắt hình nón, trụ này theo mặt phẳng chứa đường thẳng nối đỉnh và tâm hình tròn đáy của hình nón thì thu được một hình phẳng như Hình 4b.

Giải Toán 12 Bài tập cuối chương 1 - Chân trời sáng tạo

Bài 14 trang 38 Toán 12 Tập 1: Cho một hình trụ nội tiếp trong hình nón có chiều cao bằng 12 cm và bán kính đáy bằng 5 cm (Hình 4a). Người ta cắt hình nón, trụ này theo mặt phẳng chứa đường thẳng nối đỉnh và tâm hình tròn đáy của hình nón thì thu được một hình phẳng như Hình 4b.

a) Chứng minh rằng công thức tính bán kính r của đáy hình trụ theo chiều cao h của nó là: $r=\frac{5\left(12-h\right)}{12}$.

b) Chứng minh biểu thức sau biểu thị thể tích khối trụ theo h: $V\left(h\right)=\frac{25\pi h{\left(12-h\right)}^2}{144}$.

c) Tìm h để khối trụ có thể tích lớn nhất.

Lời giải:

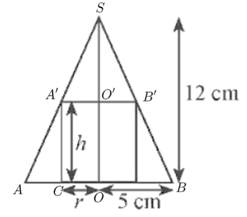
a) Ta đặt tên các điểm như hình vẽ dưới đây:

Ta có A'O' // AO nên $\frac{S{O}^{\text{'}}}{SO}=\frac{S{A}^{\text{'}}}{SA}$.

Lại có A'C // SO nên $\frac{S{A}^{\text{'}}}{SA}=\frac{OC}{OA}$.

Từ đó suy ra $\frac{S{O}^{\text{'}}}{SO}=\frac{OC}{OA}$.

Mà SO = 12 cm, OA = 5 cm, OC = r, SO' = SO – OO' = 12 – h.

Do đó, $\frac{12-h}{12}=\frac{r}{5}$. Suy ra $r=\frac{5\left(12-h\right)}{12}$.

b) Thể tích của khối trụ là V = πr²h = $\pi \cdot {\left[\frac{5\left(12-h\right)}{12}\right]}^2\cdot h=\frac{25\pi h{\left(12-h\right)}^2}{144}$(cm³).

Vậy thể tích khối trụ theo h là $V\left(h\right)=\frac{25\pi h{\left(12-h\right)}^2}{144}$.

c) Rõ ràng h phải thỏa mãn điều kiện 0 < h < 12.

Xét hàm số $V\left(h\right)=\frac{25\pi h{\left(12-h\right)}^2}{144}$ với h ∈ (0; 12).

Ta có $V^{\text{'}}\left(h\right)=\frac{25\pi \left(12-h\right)\left(12-3h\right)}{144}$.

Trên khoảng (0; 12), ta có V'(h) = 0 khi h = 4.

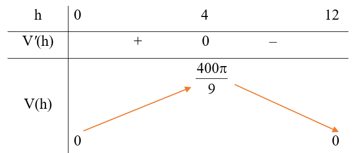
Bảng biến thiên:

Căn cứ vào bảng biến thiên, ta thấy trên khoảng (0; 12), hàm số V(h) đạt giá trị lớn nhất bằng $\frac{400\pi }{9}$ tại h = 4.

Vậy h = 4 cm thì khối trụ có thể tích lớn nhất.

Lời giải bài tập Toán 12 Bài tập cuối chương 1 hay, chi tiết khác:

• Bài 1 trang 37 Toán 12 Tập 1: Cho hàm số y = f(x) có đồ thị như Hình 1. Hàm số y = f(x) đồng biến trên khoảng ....

• Bài 2 trang 37 Toán 12 Tập 1: Cho hàm số y = f(x) có đồ thị như Hình 1 ....

• Bài 3 trang 37 Toán 12 Tập 1: Cho hàm số $y=\frac{x^2-4x+1}{x-4}$. Trong các khẳng định sau, khẳng định nào đúng? ....

• Bài 4 trang 37 Toán 12 Tập 1: Đạo hàm của hàm số y = f(x) là hàm số có đồ thị được cho trong Hình 2. Hàm số y = f(x) nghịch biến trên khoảng ....

• Bài 5 trang 37 Toán 12 Tập 1: Giá trị nhỏ nhất của hàm số $y=\sqrt{x^2+2x+3}$ trên đoạn [– 2; 3] là ....

• Bài 6 trang 37 Toán 12 Tập 1: Tiệm cận xiên của đồ thị hàm số $y=\frac{2x^3+3x^2-3}{x^2-1}$ là đường thẳng có phương trình ....

• Bài 7 trang 37 Toán 12 Tập 1: Tiệm cận đứng của đồ thị hàm số $y=\frac{-2x+3}{5x+1}$ là đường thẳng có phương trình ....

• Bài 8 trang 38 Toán 12 Tập 1: Cho hàm số $y=\frac{-2x-3}{4-x}$. Trong các khẳng định sau, khẳng định nào đúng? ....

• Bài 9 trang 38 Toán 12 Tập 1: Tìm hai số không âm a và b có tổng bằng 10 sao cho: ....

• Bài 10 trang 38 Toán 12 Tập 1: Cho hàm số bậc ba y = f(x) có đồ thị như Hình 3. Viết công thức của hàm số. ....

• Bài 11 trang 38 Toán 12 Tập 1: Cho hàm số $y=\frac{1}{3}{x}^3-x^2+4$. Khảo sát và vẽ đồ thị của hàm số. ....

• Bài 12 trang 38 Toán 12 Tập 1: Cho hàm số $y=\frac{2x+1}{x-1}$. Khảo sát và vẽ đồ thị của hàm số. ....

• Bài 13 trang 38 Toán 12 Tập 1: Cho hàm số $y=\frac{x^2+4x-1}{x-1}$. Khảo sát và vẽ đồ thị của hàm số.....

• Bài 15 trang 39 Toán 12 Tập 1: Trong một nhà hàng, mỗi tuần để chế biến x phần ăn (x lấy giá trị trong khoảng từ 30 đến 120) ....

• Bài 16 trang 39 Toán 12 Tập 1: Điện trở R(Ω) của một đoạn dây dẫn hình trụ được làm từ vật liệu có điện trở suất ρ (Ωm) ....