Giải Toán 12 trang 11 Tập 1 Chân trời sáng tạo

---

Với Giải Toán 12 trang 11 Tập 1 trong Bài 1: Tính đơn diệu và cực trị của hàm số Toán 12 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh lớp 12 dễ dàng làm bài tập Toán 12 trang 11.

Giải Toán 12 trang 11 Tập 1 Chân trời sáng tạo

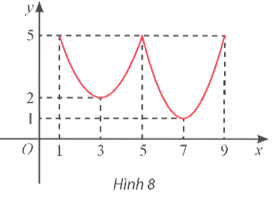
Thực hành 4 trang 11 Toán 12 Tập 1: Tìm các điểm cực trị của hàm số y = f(x) có đồ thị cho ở Hình 8.

Lời giải:

Dựa vào đồ thị ta có:

+) x = 5 là điểm cực đại của hàm số vì f(x) < f(5) với mọi x ∈ (3; 7)\{5}, y_CĐ = y(5) = 5.

+) x = 3 là điểm cực tiểu của hàm số vì f(x) > f(3) với mọi x ∈ (1; 5)\{3}, y_CT = y(3) = 2.

+) x = 7 là điểm cực tiểu của hàm số vì f(x) > f(7) với mọi x ∈ (5; 9)\{7}, y_CT = y(7) = 1.

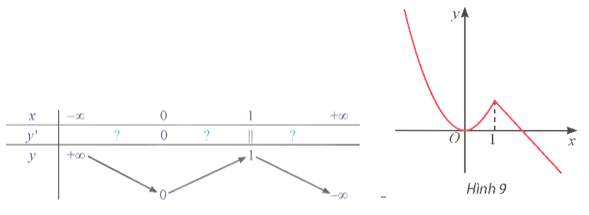
Hoạt động khám phá 3 trang 11 Toán 12 Tập 1: Đồ thị của hàm số $y=\left\{\begin{array}{l}{x}^2\text{ khi }x\le 1\\ 2-x\text{ khi }x>1\end{array}\right.$ được cho ở Hình 9.

a) Tìm điểm cực đại và điểm cực tiểu của hàm số.

b) Tại x = 1, hàm số có đạo hàm không?

c) Thay mỗi dấu ? bằng kí hiệu (+, −) thích hợp để hoàn thành bảng biến thiên dưới đây. Nhận xét về dấu của y' khi x đi qua điểm cực đại, cực tiểu.

Lời giải:

a) Dựa vào đồ thị của hàm số ta có:

+) x = 0 là điểm cực tiểu của hàm số.

+) x = 1 là điểm cực đại của hàm số.

b) Tại x = 1 hàm số không có đạo hàm.

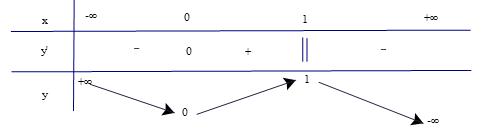
c)

Dấu của y' khi x đi qua điểm cực đại sẽ đổi từ dương sang âm.

Dấu của y' khi x đi qua điểm cực tiểu sẽ đổi từ âm sang dương.

Lời giải bài tập Toán 12 Bài 1: Tính đơn diệu và cực trị của hàm số hay khác:

• Giải Toán 12 trang 7
• Giải Toán 12 trang 9
• Giải Toán 12 trang 12
• Giải Toán 12 trang 13