Giải Toán 12 trang 9 Tập 1 Chân trời sáng tạo

---

Với Giải Toán 12 trang 9 Tập 1 trong Bài 1: Tính đơn diệu và cực trị của hàm số Toán 12 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh lớp 12 dễ dàng làm bài tập Toán 12 trang 9.

Giải Toán 12 trang 9 Tập 1 Chân trời sáng tạo

Thực hành 2 trang 9 Toán 12 Tập 1: Xét tính đơn điệu của các hàm số sau:

a) f(x) = x³ – 6x² + 9x;                                b) $g\left(x\right)=\frac{1}{x}$.

Lời giải:

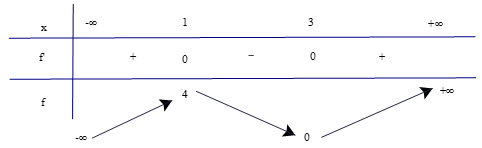
a) Tập xác định: D = ℝ.

Ta có f'(x) = 3x² – 12x + 9; f'(x) = 0 ⇔ 3x² – 12x + 9 = 0 ⇔ x = 1 hoặc x = 3.

Bảng biến thiên:

Vậy hàm số đồng biến trên các khoảng (−∞; 1) và (3; +∞), nghịch biến trên khoảng (1; 3).

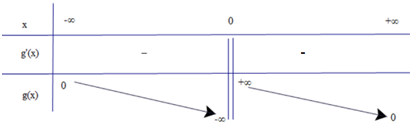
b) Tập xác định: D = ℝ\{0}.

Ta có $g^{\text{'}}\left(x\right)=-\frac{1}{x^2}<\mathrm{0,}\forall x\ne 0.$

Bảng biến thiên

Vậy hàm số nghịch biến trên các khoảng (−∞; 0) và (0; +∞).

Thực hành 3 trang 9 Toán 12 Tập 1: Chứng minh rằng hàm số f(x) = 3x – sinx đồng biến trên ℝ.

Lời giải:

Tập xác định: D = ℝ.

Ta có f'(x) = 3 – cosx.

Vì −1 ≤ cosx ≤ 1 nên −1 ≤ −cosx ≤ 1.

Do đó 2 ≤ 3 −cosx ≤ 4 hay 2 ≤ f'(x) ≤ 4.

Hay f'(x) luôn dương. Do đó hàm số f(x) = 3x – sinx đồng biến trên ℝ.

Vận dụng 1 trang 9 Toán 12 Tập 1: Hãy trả lời câu hỏi trong phần khởi động (trang 6) bằng cách xét dấu đạo hàm của hàm số h(t) = 6t³ – 81t² + 324t với 0 ≤ t ≤ 8.

Lời giải:

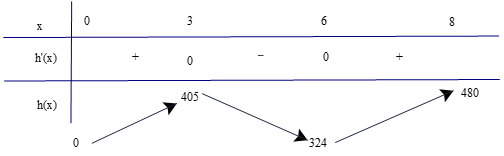
Tập xác định: D = ℝ.

Ta có h'(t) = 18t² – 162t + 324; h'(t) = 0 ⇔ 18t² – 162t + 324 = 0 ⇔ t = 3 hoặc t = 6.

Bảng biến thiên

Dựa vào bảng biến thiên ta có:

Trong khoảng thời gian (0; 3) và (6; 8) thì khinh khí cầu tăng dần độ cao và trong khoảng (3; 6) thì khinh khí cầu giảm dần độ cao.

Lời giải bài tập Toán 12 Bài 1: Tính đơn diệu và cực trị của hàm số hay khác:

• Giải Toán 12 trang 7
• Giải Toán 12 trang 11
• Giải Toán 12 trang 12
• Giải Toán 12 trang 13