Giải Toán 12 trang 61 Tập 2 Chân trời sáng tạo

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 12 trang 61 Tập 2 trong Bài 3: Phương trình mặt cầu Toán 12 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 61.

Giải Toán 12 trang 61 Tập 2 Chân trời sáng tạo

Hoạt động khởi động trang 61 Toán 12 Tập 2:

Ta đã biết trong mặt phẳng tọa độ Oxy, phương trình đường tròn tâm I(a; b), bán kính R có dạng: (x – a)² + (y – b)² = R².

Trong không gian Oxyz, phương trình mặt cầu có dạng như thế nào?

Lời giải:

Trong không gian Oxyz, mặt cầu (S) tâm I(a; b; c), bán kính R có phương trình là:

(x – a)² + (y – b)² + (z – c)² = R².

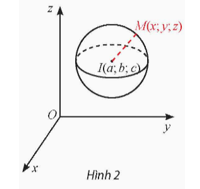
Hoạt động khám phá 1 trang 61 Toán 12 Tập 2: Trong không gian Oxyz, cho mặt cầu S(I; R) có tâm I(a; b; c) và bán kính R. Xét một điểm M(x; y; z) thay đổi.

a) Tính khoảng cách IM theo x, y, z và a, b, c.

b) Nêu điều kiện cần và đủ của x, y, z để điểm M(x; y; z) nằm trên mặt cầu S(I; R).

Lời giải:

a) Ta có $IM=\sqrt{{\left(x-a\right)}^2+{\left(y-b\right)}^2+{\left(z-c\right)}^2}$.

b) Để điểm M(x; y; z) nằm trên mặt cầu S(I; R) ⇔ IM = R

$\sqrt{{\left(x-a\right)}^2+{\left(y-b\right)}^2+{\left(z-c\right)}^2}=R$ hay (x – a)² + (y – b)² + (z – c)² = R².

Lời giải bài tập Toán 12 Bài 3: Phương trình mặt cầu hay khác:

• Giải Toán 12 trang 62
• Giải Toán 12 trang 63
• Giải Toán 12 trang 64
• Giải Toán 12 trang 65