Giải Toán 12 trang 12 Tập 1 Kết nối tri thức

---

Với Giải Toán 12 trang 12 Tập 1 trong Bài 1: Tính đơn điệu và cực trị của hàm số Toán 12 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 12.

Giải Toán 12 trang 12 Tập 1 Kết nối tri thức

Luyện tập 5 trang 12 Toán 12 Tập 1: Tìm cực trị của các hàm số sau:

a) y = x⁴ – 3x² + 1;                                     b) $y=\frac{-x^2+2x-1}{x+2}$.

Lời giải:

a) Tập xác định của hàm số là ℝ.

Ta có y' = 4x³ – 6x; y' = 0 ⇔ x = 0 hoặc x = $-\frac{\sqrt{6}}{2}$ hoặc x = 0 hoặc $x=\frac{\sqrt{6}}{2}$.

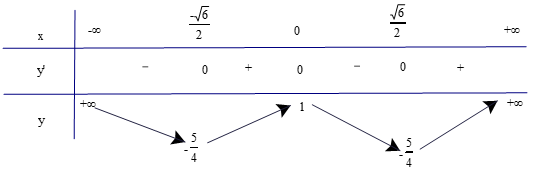
Lập bảng biến thiên của hàm số

Từ bảng biến thiên ta có:

Hàm số đạt cực tiểu tại $x=-\frac{\sqrt{6}}{2}$ và y_CT = $-\frac{5}{4}$.

Hàm số đạt cực đại tại x = 0 và y_CĐ = 1.

Hàm số đạt cực tiểu tại $x=\frac{\sqrt{6}}{2}$ và y_CT = $-\frac{5}{4}$.

b) Tập xác định của hàm số là ℝ\{−2}.

Có $y^{\text{'}}=\frac{\left(-2x+2\right)\left(x+2\right)-\left(-x^2+2x-1\right)}{{\left(x+2\right)}^2}=\frac{-x^2-4x+5}{{\left(x+2\right)}^2}$.

Có y' = 0⇔ −x² – 4x + 5 = 0 ⇔ x = 1 hoặc x = −5.

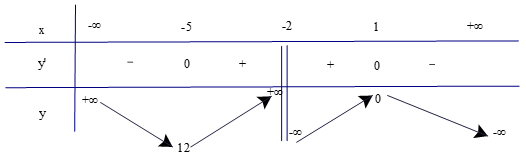
Lập bảng biến thiên của hàm số

Từ bảng biến thiên ta có:

Hàm số đạt cực tiểu tại x = −5 và y_CT = 12.

Hàm số đạt cực đại tại x = 1 và y_CĐ = 0.

Vận dụng 2 trang 12 Toán 12 Tập 1: Một vật được phóng thẳng đứng lên trên từ độ cao 2m với vận tốc ban đầu là 24,5 m/s. Trong Vật lí, ta biết rằng khi bỏ qua sức cản của không khí thì độ cao h (mét) của vật sau t (giây) được cho bởi công thức

h(t) = 2 + 24,5t – 4,9t².

Hỏi tại thời điểm nào thì vật đạt độ cao lớn nhất?

Lời giải:

Tập xác định của hàm số là ℝ.

Có h'(t) = −9,8t + 24,5; h'(t) = 0 ⇔ $t=\frac{5}{2}$.

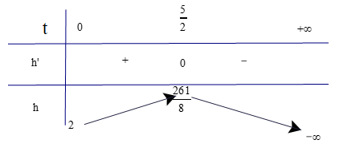
Lập bảng biến thiên của hàm số

Dựa vào bảng biến thiên ta có tại thời điểm $t=\frac{5}{2}$ thì vật đạt độ cao lớn nhất là $\frac{261}{8}$.

Lời giải bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số hay khác:

• Giải Toán 12 trang 6
• Giải Toán 12 trang 7
• Giải Toán 12 trang 9
• Giải Toán 12 trang 10
• Giải Toán 12 trang 13
• Giải Toán 12 trang 14