Giải Toán 12 trang 13 Tập 1 Kết nối tri thức

---

Với Giải Toán 12 trang 13 Tập 1 trong Bài 1: Tính đơn điệu và cực trị của hàm số Toán 12 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 13.

Giải Toán 12 trang 13 Tập 1 Kết nối tri thức

Bài 1.1 trang 13 Toán 12 Tập 1: Tìm các khoảng đồng biến, khoảng nghịch biến của các hàm số có đồ thị như sau:

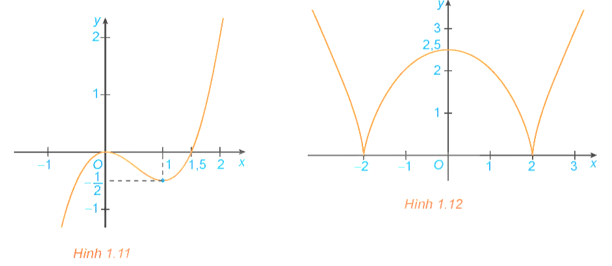
a) Đồ thị hàm số $y=x^3-\frac{3}{2}{x}^2$ (H.1.11);

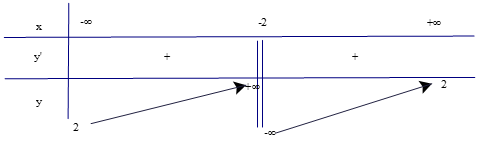
b) Đồ thị hàm số $y=\sqrt[3]{{\left(x^2-4\right)}^2}$ (H.1.12).

Lời giải:

a) Dựa vào đồ thị hàm số ta có:

Hàm số đồng biến trên các khoảng (−∞; 0) và (1; +∞).

Hàm số nghịch biến trên khoảng (0; 1).

b) Dựa vào đồ thị hàm số ta có:

Hàm số đồng biến trên các khoảng (−2; 0) và (2; +∞).

Hàm số nghịch biến trên các khoảng (−∞; −2) và (0; 2).

Bài 1.2 trang 13 Toán 12 Tập 1: Xét sự đồng biến, nghịch biến của các hàm số sau:

a) $y=\frac{1}{3}{x}^3-2x^2+3x+1$;

b) y = −x³ + 2x² – 5x + 3.

Lời giải:

a) Tập xác định của hàm số là ℝ.

Có y' = x² – 4x + 3.

Hàm số đồng biến khi y' > 0 $\iff$ x² – 4x + 3 > 0 $\iff \left[\begin{array}{l}x<1\\ x>3\end{array}\right.$.

Hàm số nghịch biến khi y' < 0 $\iff$ x² – 4x + 3 < 0 $\iff$ 1 < x < 3.

Do đó hàm số đồng biến trên các khoảng (−∞; 1) và (3; +∞); nghịch biến trên khoảng (1; 3).

b) Tập xác định của hàm số là ℝ.

Có y' = −3x² + 4x – 5

$\begin{array}{l}=-3\left(x^2-\frac{4}{3}x\right)-5\\ =-3\left(x^2-\frac{4}{3}x+\frac{4}{9}\right)+\frac{4}{3}-5\\ =-3{\left(x-\frac{2}{3}\right)}^2-\frac{11}{3}<\mathrm{0,}\forall x\end{array}$

Do đó hàm số luôn nghịch biến.

Bài 1.3 trang 13 Toán 12 Tập 1: Tìm các khoảng đơn điệu của các hàm số sau:

a) $y=\frac{2x-1}{x+2}$;                                               b) $y=\frac{x^2+x+4}{x-3}$.

Lời giải:

a) Tập xác định của hàm số là ℝ\{−2}.

Có $y^{\text{'}}=\frac{2\left(x+2\right)-\left(2x-1\right)}{{\left(x+2\right)}^2}=\frac{5}{{\left(x+2\right)}^2}>\mathrm{0,}\forall x\ne -2$.

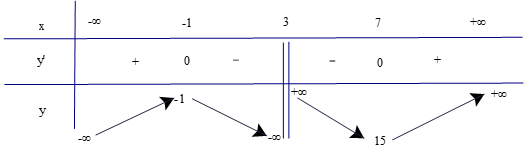
Lập bảng biến thiên của hàm số

Dựa vào bảng biến thiên ta có:

Hàm số đồng biến trên cách khoảng (−∞; −2) và (−2; +∞).

b) Tập xác định của hàm số là ℝ\{3}.

Có $y^{\text{'}}=\frac{\left(2x+1\right)\left(x-3\right)-\left(x^2+x+4\right)}{{\left(x-3\right)}^2}=\frac{x^2-6x-7}{{\left(x-3\right)}^2}$;

Có y' = 0 ⇔ x² – 6x – 7 = 0 ⇔ x = −1 hoặc x = 7.

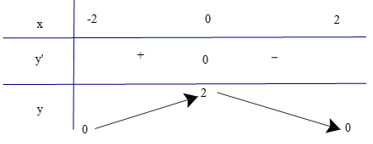
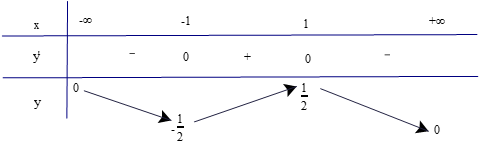
Lập bảng biến thiên của hàm số

Từ bảng biến thiên, ta có:

Hàm số đồng biến trên các khoảng (−∞; −1) và (7; +∞).

Hàm số nghịch biến trên các khoảng (−1; 3) và (3; 7).

Bài 1.4 trang 13 Toán 12 Tập 1: Xét chiều biến thiên của các hàm số sau:

a) $y=\sqrt{4-x^2}$;                                            b) $y=\frac{x}{x^2+1}$.

Lời giải:

a) Tập xác định của hàm số là D = [−2; 2].

Có $y^{\text{'}}=\frac{{\left(4-x^2\right)}^{\text{'}}}{2\sqrt{4-x^2}}=\frac{-x}{\sqrt{4-x^2}};$ y' = 0 ⇔ x = 0.

Lập bảng biến thiên của hàm số

Dựa vào bảng biến thiên, ta có

Hàm số đồng biến trên khoảng (−2; 0) và nghịch biến trên khoảng (0; 2).

b) Tập xác định của hàm số là ℝ.

Có $y^{\text{'}}=\frac{\left(x^2+1\right)-2x^2}{{\left(x^2+1\right)}^2}=\frac{-x^2+1}{{\left(x^2+1\right)}^2}$; y' = 0 ⇔ −x² + 1 = 0 ⇔ x = 1 hoặc x = −1.

Lập bảng biến thiên của hàm số

Dựa vào bảng biến thiên, ta có:

Hàm số đồng biến trên khoảng (−1; 1).

Hàm số nghịch biến trên các khoảng (−∞; −1) và (1; +∞).

Bài 1.5 trang 13 Toán 12 Tập 1: Giả sử số dân của một thị trấn sau t năm kể từ năm 2000 được mô tả bởi hàm số $N\left(t\right)=\frac{25t+10}{t+5},t\ge \mathrm{0,}$ trong đó N(t) được tính bằng nghìn người.

a) Tính số dân của thị trấn đó vào các năm 2000 và 2015.

b) Tính đạo hàm N'(t) và $\underset{t\to +\infty }{\lim }N\left(t\right)$. Từ đó, giải thích tại sao số dân của thị trấn đó luôn tăng nhưng sẽ không vượt quá một ngưỡng nào đó.

Lời giải:

a) Số dân vào năm 2000 (t = 0) của thị trấn đó là: $N\left(0\right)=\frac{25.0+10}{0+5}=2$ nghìn người.

Sau 15 năm kể từ năm 2000 số dân của thị trấn đó là: $N\left(15\right)=\frac{25.15+10}{15+5}=\mathrm{19,25}$.

Vậy số dân của thị trấn đó vào năm 2015 là 19250 người.

b) Có $N^{\text{'}}\left(t\right)=\frac{25\left(t+5\right)-\left(25t+10\right)}{{\left(t+5\right)}^2}=\frac{115}{{\left(t+5\right)}^2}$;

$\underset{t\to +\infty }{\lim }N\left(t\right)=\underset{t\to +\infty }{\lim }\frac{25t+10}{t+5}=\underset{t\to +\infty }{\lim }\frac{25+\frac{10}{t}}{1+\frac{5}{t}}=25$

Vì N'(t) > 0, ∀t do đó hàm số N(t) là hàm đồng biến hơn nữa $\underset{t\to +\infty }{\lim }N\left(t\right)=25$ do đó dân số của thị trấn đó sẽ không vượt quá 25 nghìn người.

Lời giải bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số hay khác:

• Giải Toán 12 trang 6
• Giải Toán 12 trang 7
• Giải Toán 12 trang 9
• Giải Toán 12 trang 10
• Giải Toán 12 trang 12
• Giải Toán 12 trang 14