Giải Toán 12 trang 9 Tập 1 Kết nối tri thức

---

Với Giải Toán 12 trang 9 Tập 1 trong Bài 1: Tính đơn điệu và cực trị của hàm số Toán 12 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 9.

Giải Toán 12 trang 9 Tập 1 Kết nối tri thức

Luyện tập 3 trang 9 Toán 12 Tập 1: Tìm các khoảng đơn điệu của các hàm số sau:

a) $y=\frac{1}{3}{x}^3+3x^2+5x+2;$                            b) $y=\frac{-x^2+5x-7}{x-2}$.

Lời giải:

a) Tập xác định của hàm số là ℝ.

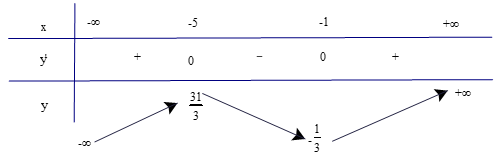
Ta có y' = x² + 6x + 5; y' = 0 Û x = −1 hoặc x = −5.

Lập bảng biến thiên của hàm số

Từ bảng biến thiên ta có:

Hàm số đồng biến trên các khoảng (−∞; −5) và (−1; +∞).

Hàm số nghịch biến trên khoảng (−5; −1).

b) Tập xác định của hàm số là ℝ\{2}.

Có $y^{\text{'}}=\frac{\left(-2x+5\right)\left(x-2\right)-\left(-x^2+5x-7\right)}{{\left(x-2\right)}^2}=\frac{-x^2+4x-3}{{\left(x-2\right)}^2}$;

y' = 0 ⇔ x = 3 hoặc x = 1.

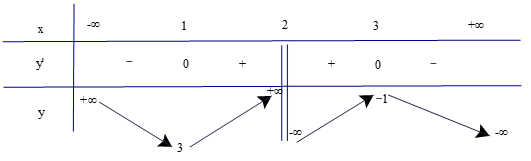
Lập bảng biến thiên của hàm số

Từ bảng biến thiên ta có:

Hàm số đồng biến trên các khoảng (1; 2) và (2; 3).

Hàm số nghịch biến trên các khoảng (−∞; 1) và (3; +∞).

Vận dụng 1 trang 9 Toán 12 Tập 1: Giải bài toán trong tình huống mở đầu bằng cách thực hiện lần lượt các yêu cầu sau:

Lời giải:

a) Theo ý nghĩa cơ học của đạo hàm, vận tốc v(t) là đạo hàm của s(t). Hãy tìm vận tốc v(t).

b) Xét dấu của hàm v(t), từ đó suy ra câu trả lời.

Lời giải:

a) s(t) = t³ – 9t² + 15t.

Có v(t) = s'(t) = 3t² – 18t + 15.

b) Có v(t) > 0 $\iff \left[\begin{array}{l}t<1\\ t>5\end{array}\right.$ và v(t) < 0 $\iff$1 < t < 5.

Chất điểm chuyển động sang phải khi t ∈ (0; 1) và (5; +∞).

Chất điểm chuyển động sang trái khi t ∈ (1; 5).

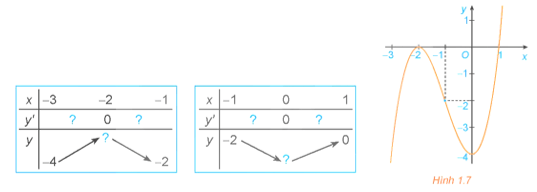
HĐ4 trang 9 Toán 12 Tập 1: Quan sát đồ thị của hàm số y = x³ + 3x² – 4 (H.1.7). Xét dấu đạo hàm của hàm số đã cho và hoàn thành các bảng sau vào vở:

Lời giải:

Tập xác định của hàm số là ℝ.

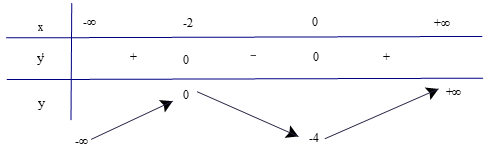
Có y' = 3x² + 6x; y' = 0 $\iff$ x = 0 hoặc x = −2.

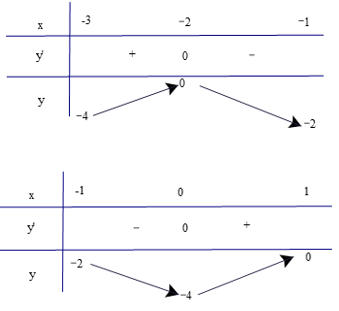
Ta có bảng biến thiên

Dựa vào bảng biến thiên trên, ta có

Lời giải bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số hay khác:

• Giải Toán 12 trang 6
• Giải Toán 12 trang 7
• Giải Toán 12 trang 10
• Giải Toán 12 trang 12
• Giải Toán 12 trang 13
• Giải Toán 12 trang 14