Giải Toán 12 trang 13 Tập 2 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 12 trang 13 Tập 2 trong Bài 12: Tích phân Toán 12 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 13.

Giải Toán 12 trang 13 Tập 2 Kết nối tri thức

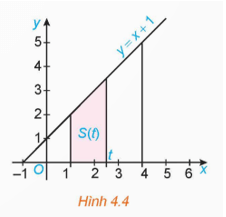
HĐ1 trang 13 Toán 12 Tập 2: Kí hiệu T là hình thang vuông giới hạn bởi đường thẳng y = x + 1, trục hoành và hai đường thẳng x = 1, x = t (1 ≤ t ≤ 4) (H.4.4)

a) Tính diện tích S của T khi t = 4.

b) Tính diện tích S(t) của T khi t ∈ [1; 4].

c) Chứng minh rằng S(t) là một nguyên hàm của hàm số f(t) = t + 1, t ∈ [1; 4] và diện tích S = S(4) – S(1).

Lời giải:

a)

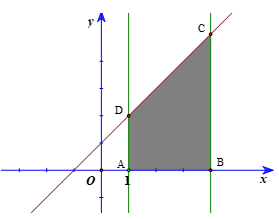
Kí hiệu A(1; 0), B(4; 0) và C, D lần lượt là giao điểm của đường thẳng x = 4; x = 1 với đường thẳng y = x + 1.

Khi đó C(4; 5), D(1; 2).

Ta có: AD = 2; BC = 5; AB = 3.

Khi đó diện tích hình thang T là $S=\frac{\left(AD+BC\right).AB}{2}=\frac{\left(2+5\right).3}{2}=\frac{21}{2}$.

b)

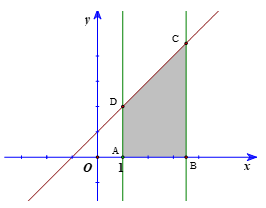
Gọi A(1; 0), B(t; 0), t ∈ [1; 4] và C, D lần lượt là giao điểm của đường thẳng x = t; x = 1 với đường thẳng y = x + 1.

Khi đó C(t; t + 1); D(1; 2).

Do đó AB = t – 1; AD = 2; BC = t + 1.

Khi đó diện tích hình thang ABCD là

$S\left(t\right)=\frac{\left(AD+BC\right).AB}{2}=\frac{\left(t+3\right).\left(t-1\right)}{2}=\frac{t^2+2t-3}{2}.$

c) Có $S\left(t\right)=\frac{t^2+2t-3}{2}$$\Rightarrow S^{\text{'}}\left(t\right)={\left(\frac{t^2+2t-3}{2}\right)}^{\text{'}}=\frac{2\left(t+1\right)}{2}=t+1=f\left(t\right)$

Do đó S(t) là một nguyên hàm của hàm số f(t) = t + 1, t ∈ [1; 4].

Có $S\left(4\right)=\frac{4^2+2.4-3}{2}=\frac{21}{2};S\left(1\right)=\frac{1^2+2.1-3}{2}=0$

Do đó S(4) – S(1) = S.

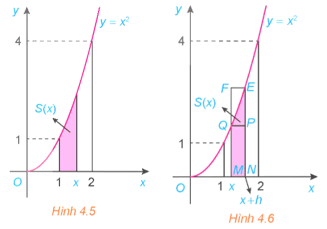
HĐ2 trang 13 Toán 12 Tập 2: Xét hình thang cong giới hạn bởi đồ thị y = x², trục hoành và hai đường thẳng x = 1, x = 2. Ta muốn tính diện tích S của hình thang cong này.

a) Với mỗi x ∈ [1; 2], gọi S(x) là diện tích phần hình thang cong đã cho nằm giữa hai đường thẳng vuông góc với trục Ox tại điểm có hoành độ bằng 1 và x (H.4.5).

Cho h > 0 sao cho x + h < 2. So sánh hiệu S(x + h) – S(x) với diện tích hai hình chữ nhật MNPQ và MNEF (H.4.6). Từ đó suy ra $0\le \frac{S\left(x+h\right)-S\left(x\right)}{h}-x^2\le 2xh+h^2$

b) Cho h < 0 sao cho x + h > 1. Tương tự phần a, đánh giá hiệu S(x) – S(x + h) và từ đó suy ra $2xh+h^2\le \frac{S\left(x+h\right)-S\left(x\right)}{h}-x^2\le 0$

c) Từ kết quả phần a và phần b, suy ra với mọi h ≠ 0, ta có $\left|\frac{S\left(x+h\right)-S\left(x\right)}{h}-x^2\right|\le 2x\left|h\right|+h^2$.

Từ đó chứng minh S'(x) = x², x ∈ (1; 2).

Người ta chứng minh được S'(1) = 1, S'(2) = 4, tức là S(x) là một nguyên hàm của x² trên [1; 2].

d) Từ kết quả của phần c, ta có $S\left(x\right)=\frac{x^3}{3}+C$. Sử dụng điều này với lưu ý S(1) = 0 và diện tích cần tính S = S(2), hãy tính S.

Gọi F(x) là một nguyên hàm tùy ý của f(x) = x² trên [1; 2]. Hãy so sánh S và F(2) – F(1).

Lời giải:

a) Với h > 0, x + h < 2, kí hiệu S_MNPQ và S_MNEF lần lượt là diện tích các hình chữ nhật MNPQ và MNEF, ta có: S_MNPQ ≤ S(x + h) – S(x) ≤ S_MNEF

hay hx² ≤ S(x + h) – S(x) ≤ h(x + h)².

Suy ra $0\le \frac{S\left(x+h\right)-S\left(x\right)}{h}-x^2\le 2xh+h^2$

b) Với h < 0 và x + h > 1, kí hiệu S_MNPQ và S_MNEF lần lượt là diện tích các hình chữ nhật MNPQ và MNEF, ta có S_MNPQ ≤ S(x + h) – S(x) ≤ S_MNEF

hay h(x+h)² ≤ S(x + h) – S(x) ≤ hx².

Suy ra $2xh+h^2\le \frac{S\left(x+h\right)-S\left(x\right)}{h}-x^2\le 0$

c) Dựa vào kết quả của câu a, b ta suy ra với mọi h ≠ 0, ta có:

$\left|\frac{S\left(x+h\right)-S\left(x\right)}{h}-x^2\right|\le 2x\left|h\right|+h^2$

Suy ra $S^{\text{'}}\left(x\right)=\underset{h\to 0}{\lim }\frac{S\left(x+h\right)-S\left(x\right)}{h}=x^2,\forall x\in \left(1;2\right)$

d) Vì S(1) = 0 nên $S\left(1\right)=\frac{1^3}{3}+C=0\Rightarrow C=-\frac{1}{3}$

Vậy $S\left(x\right)=\frac{x^3}{3}-\frac{1}{3}$

Ta có $S=S\left(2\right)=\frac{2^3}{3}-\frac{1}{3}=\frac{7}{3}$

Giả sử $F\left(x\right)=\frac{x^3}{3}$ là một nguyên hàm của f(x) = x² trên [1; 2].

Khi đó $F\left(1\right)=\frac{1}{3};F\left(2\right)=\frac{8}{3}$. Ta thấy $F\left(2\right)-F\left(1\right)=\frac{7}{3}=S$.

Lời giải bài tập Toán 12 Bài 12: Tích phân hay khác:

• Giải Toán 12 trang 16
• Giải Toán 12 trang 17
• Giải Toán 12 trang 18