Giải Toán 12 trang 18 Tập 2 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 12 trang 18 Tập 2 trong Bài 12: Tích phân Toán 12 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 18.

Giải Toán 12 trang 18 Tập 2 Kết nối tri thức

Bài 4.8 trang 18 Toán 12 Tập 2: Sử dụng ý nghĩa hình học của tích phân, tính:

a) $\underset{1}{\overset{2}{\int }}\left(2x+1\right)dx$

b) $\underset{-3}{\overset{3}{\int }}\sqrt{9-x^2}dx$

Lời giải:

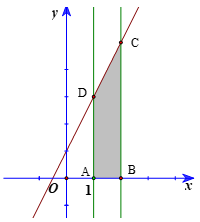
a)

Gọi A(1; 0), B(2; 0) và C, D lần lượt là giao điểm của đường thẳng x = 2; x = 1 với đường thẳng y = 2x + 1. Khi đó C(2; 5), D(1; 3).

Tích phân cần tính chính là diện tích của hình thang vuông ABCD với đáy nhỏ AD = 3, đáy lớn BC = 5, đường cao AB = 1.

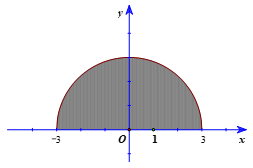
Khi đó $\underset{1}{\overset{2}{\int }}\left(2x+1\right)dx=S_{ABCD}=\frac{\left(AD+BC\right)AB}{2}=\frac{\left(3+5\right).1}{2}=4$

b)

Ta có $y=\sqrt{9-x^2}$ là phương trình nửa phía trên trục hoành của đường tròn tâm tại gốc tọa độ O và bán kính 3. Do đó, tích phân cần tính là diện tích nửa phía trên trục hoành của hình tròn tương ứng.

Vậy $\underset{-3}{\overset{3}{\int }}\sqrt{9-x^2}dx=\frac{1}{2}.\pi {.3}^2=\frac{9}{2}\pi$

Bài 4.9 trang 18 Toán 12 Tập 2: Cho $\underset{0}{\overset{3}{\int }}f\left(x\right)dx=5$ và $\underset{0}{\overset{3}{\int }}g\left(x\right)dx=2$. Tính:

a) $\underset{0}{\overset{3}{\int }}\left[f\left(x\right)+g\left(x\right)\right]dx$;

b) $\underset{0}{\overset{3}{\int }}\left[f\left(x\right)-g\left(x\right)\right]dx$;

c) $\underset{0}{\overset{3}{\int }}3f\left(x\right)dx$;

d) $\underset{0}{\overset{3}{\int }}\left[2f\left(x\right)-3g\left(x\right)\right]dx$

Lời giải:

a) $\underset{0}{\overset{3}{\int }}\left[f\left(x\right)+g\left(x\right)\right]dx$$=\underset{0}{\overset{3}{\int }}f\left(x\right)dx+\underset{0}{\overset{3}{\int }}g\left(x\right)dx=5+2=7$

b) $\underset{0}{\overset{3}{\int }}\left[f\left(x\right)-g\left(x\right)\right]dx$$=\underset{0}{\overset{3}{\int }}f\left(x\right)dx-\underset{0}{\overset{3}{\int }}g\left(x\right)dx=5-2=3$

c) $\underset{0}{\overset{3}{\int }}3f\left(x\right)dx$$=3\underset{0}{\overset{3}{\int }}f\left(x\right)dx=3.5=15$

d) $\underset{0}{\overset{3}{\int }}\left[2f\left(x\right)-3g\left(x\right)\right]dx$$=2\underset{0}{\overset{3}{\int }}f\left(x\right)dx-3\underset{0}{\overset{3}{\int }}g\left(x\right)dx$$=2.5-3.2=4$

Bài 4.10 trang 18 Toán 12 Tập 2: Tính:

a) $\underset{0}{\overset{3}{\int }}{\left(3x-1\right)}^{2}dx$;

b) $\underset{0}{\overset{\frac{\pi }{2}}{\int }}\left(1+\sin x\right)dx$;

c) $\underset{0}{\overset{1}{\int }}\left(e^{2x}+3x^2\right)dx$;

d) $\underset{-1}{\overset{2}{\int }}\left|2x+1\right|dx$

Lời giải:

a) $\underset{0}{\overset{3}{\int }}{\left(3x-1\right)}^{2}dx$$=\underset{0}{\overset{3}{\int }}\left(9x^2-6x+1\right)dx$$=9\underset{0}{\overset{3}{\int }}{x}^{2}dx-6\underset{0}{\overset{3}{\int }}xdx+\underset{0}{\overset{3}{\int }}dx$

$={\left.3x^3\right|}_0^3-{\left.3x^2\right|}_0^3+{\left.x\right|}_0^3$$=81-27+3=57$

b) $\underset{0}{\overset{\frac{\pi }{2}}{\int }}\left(1+\sin x\right)dx$$=\underset{0}{\overset{\frac{\pi }{2}}{\int }}dx+\underset{0}{\overset{\frac{\pi }{2}}{\int }}\sin xdx$$={\left.x\right|}_0^{\frac{\pi }{2}}-{\left.\cos x\right|}_0^{\frac{\pi }{2}}$$=\frac{\pi }{2}+1$

c) $\underset{0}{\overset{1}{\int }}\left(e^{2x}+3x^2\right)dx$$=\underset{0}{\overset{1}{\int }}{e}^{2x}dx+3\underset{0}{\overset{1}{\int }}{x}^{2}dx$$={\left.\frac{e^{2x}}{2}\right|}_0^1+{\left.x^3\right|}_0^1$$=\frac{e^2}{2}-\frac{1}{2}+1=\frac{e^2}{2}+\frac{1}{2}$

d) $\underset{-1}{\overset{2}{\int }}\left|2x+1\right|dx$$=\underset{-1}{\overset{\frac{-1}{2}}{\int }}\left|2x+1\right|dx+\underset{\frac{-1}{2}}{\overset{2}{\int }}\left|2x+1\right|dx$$=\underset{-1}{\overset{\frac{-1}{2}}{\int }}\left(-2x-1\right)dx+\underset{\frac{-1}{2}}{\overset{2}{\int }}\left(2x+1\right)dx$

$={\left.\left(-x^2-x\right)\right|}_{-1}^{\frac{-1}{2}}+{\left.\left(x^2+x\right)\right|}_{\frac{-1}{2}}^2$$=\frac{1}{4}+6+\frac{1}{4}=\frac{13}{2}$

Bài 4.11 trang 18 Toán 12 Tập 2: Một vật chuyển động dọc theo một đường thẳng sao cho vận tốc của nó tại thời điểm t (giây) là v(t) = t² – t – 6 (m/s).

Lời giải:

a) Tìm độ dịch chuyển của vật trong khoảng thời gian 1 ≤ t ≤ 4, tức là tính $\underset{1}{\overset{4}{\int }}v\left(t\right)dt$.

b) Tìm tổng quãng đường vật đi được trong khoảng thời gian này, tức là tính $\underset{1}{\overset{4}{\int }}\left|v\left(t\right)\right|dt.$

Lời giải:

a) Độ dịch chuyển của vật trong khoảng thời gian 1 ≤ t ≤ 4 là

$\underset{1}{\overset{4}{\int }}v\left(t\right)dt=\underset{1}{\overset{4}{\int }}\left(t^2-t-6\right)dt$$=\underset{1}{\overset{4}{\int }}{t}^{2}dt-\underset{1}{\overset{4}{\int }}tdt-6\underset{1}{\overset{4}{\int }}dt$$={\left.\left(\frac{t^3}{3}-\frac{t^2}{2}-6t\right)\right|}_1^4$$=-\frac{32}{3}+\frac{37}{6}=-\frac{9}{2}$

b) Tổng quãng đường vật đi được trong khoảng thời gian này là

$\underset{1}{\overset{4}{\int }}\left|v\left(t\right)\right|dt$$=\underset{1}{\overset{4}{\int }}\left|t^2-t-6\right|dt$$=\underset{1}{\overset{3}{\int }}\left|t^2-t-6\right|dt+\underset{3}{\overset{4}{\int }}\left|t^2-t-6\right|dt$

$=-\underset{1}{\overset{3}{\int }}\left(t^2-t-6\right)dt+\underset{3}{\overset{4}{\int }}\left(t^2-t-6\right)dt$$=-{\left.\left(\frac{t^3}{3}-\frac{t^2}{2}-6t\right)\right|}_1^3+{\left.\left(\frac{t^3}{3}-\frac{t^2}{2}-6t\right)\right|}_3^4$

$=\frac{27}{2}-\frac{37}{6}-\frac{32}{3}+\frac{27}{2}=\frac{61}{6}$

Bài 4.12 trang 18 Toán 12 Tập 2: Giả sử lợi nhuận biên (tính bằng triệu đồng) của một sản phẩm được mô hình hóa bằng công thức P'(x) = −0,0005x + 12,2. Ở đây P(x) là lợi nhuận (tính bằng triệu đồng) khi bán được x đơn vị sản phẩm.

a) Tìm sự thay đổi của lợi nhuận khi doanh số tăng từ 100 lên 101 sản phẩm.

b) Tìm sự thay đổi của lợi nhuận khi doanh số tăng từ 100 lên 110 sản phẩm.

Lời giải:

a) Sự thay đổi của lợi nhuận khi doanh số tăng từ 100 lên 101 sản phẩm là:

$\underset{100}{\overset{101}{\int }}{P}^{\text{'}}\left(x\right)dx=\underset{100}{\overset{101}{\int }}\left(-\mathrm{0,0005}x+\mathrm{12,2}\right)dx$$={\left.\left(-\frac{1}{4000}{x}^2+\mathrm{12,2}x\right)\right|}_{100}^{101}$

= 1229,64975 – 1217,5 = 12,14975 triệu đồng.

b) Sự thay đổi của lợi nhuận khi doanh số tăng từ 100 lên 110 sản phẩm là

$\underset{100}{\overset{110}{\int }}{P}^{\text{'}}\left(x\right)dx=\underset{100}{\overset{110}{\int }}\left(-\mathrm{0,0005}x+\mathrm{12,2}\right)dx$$={\left.\left(-\frac{1}{4000}{x}^2+\mathrm{12,2}x\right)\right|}_{100}^{110}$

= 1338,975 – 1217,5 = 121,475 triệu đồng.

Bài 4.13 trang 18 Toán 12 Tập 2: Giả sử vận tốc v của dòng máu ở khoảng cách r từ tâm của động mạch bán kính R không đổi, có thể được mô hình hóa bởi công thức v = k(R² – r²), trong đó k là một hằng số. Tìm vận tốc trung bình (đối với r) của động mạch trong khoảng 0 ≤ r ≤ R. So sánh vận tốc trung bình với vận tốc lớn nhất.

Lời giải:

Vận tốc trung bình của động mạch là:

$v_{tb}=\frac{1}{R-0}\underset{0}{\overset{R}{\int }}v\left(r\right)dr$$=\frac{1}{R}\underset{0}{\overset{R}{\int }}k\left(R^2-r^2\right)dr$$={\left.\frac{1}{R}k\left(R^{2}r-\frac{r^3}{3}\right)\right|}_0^R$$=\frac{2}{3}k{R}^2$

Do đó, vận tốc trung bình của động mạch là $\frac{2}{3}k{R}^2$

Vì 0 ≤ r ≤ R nên vận tốc lớn nhất của động mạch là kR² khi r = 0.

Do đó $v_{tb}=\frac{2}{3}{v}_{\max }$

Lời giải bài tập Toán 12 Bài 12: Tích phân hay khác:

• Giải Toán 12 trang 13
• Giải Toán 12 trang 16
• Giải Toán 12 trang 17